Bonjour,
Je suis en train de me casser la tête sur mon cr de physique.
Le tp parle de la chute libre d'une bille après la sortie de cette dernière d'une glissière.
On utilise l'ordi pour modeliser les courbe de x(t), y(t) et y(x)...
Bon on obtient des modelisations de la forme :
x(t)=at+b
y(t)=ct^2+dt+e
y(x)=fx^2+gx+h
Ils nous disent dans le fascicule que les équations théoriques sont x=v(0)t; y=(g/2)t^2 et y(x)=(g/(2v(0)^2)t^2. Ils demandent donc lors de l'experience pourquoi b,d,e,g et h ne sont pas nuls et queelle interprétation physique peut on leur donner !
Qui peut m'espliquer et me dire la réponce ?
Merci d'avance
Masha
Mecanique cr à rendre le 7 decembre
4 messages
- Page 1 sur 1
bonsoir,
équation vectorielle : = \vec{g}t^2/2 + \vec v_0 t + \vec{OM_0})
projetée sur Ox : = x'_0 t + x_0)
projetée sur Oy : = g t^2/2 + y'_0 t + y_0)
en éliminant t entre ces 2 équations :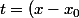/x'_0)
 = g (x-x_0)^2 /x'_0^2 /2 + y'_0 (x-x_0)/x'_0 + y_0)
y(x) = ...
en comparant avec tes formules :
x(t)=at+b
y(t)=ct^2+dt+e
y(x)=fx^2+gx+h
on voit que (b,e) est) la position initiale de la bille
la position initiale de la bille
(a,d) est) la vitesse initiale de la bille
la vitesse initiale de la bille
pour e et g, il faudrait développer y(x)
équation vectorielle :
projetée sur Ox :
projetée sur Oy :
en éliminant t entre ces 2 équations :
y(x) = ...
en comparant avec tes formules :
x(t)=at+b
y(t)=ct^2+dt+e
y(x)=fx^2+gx+h
on voit que (b,e) est
(a,d) est
pour e et g, il faudrait développer y(x)
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
