Bonjour , j'ai beaucoup de mal a comprendre comment entamer mon exercice , car il s'agit de deux suites sous forme de système ...
L'exercice :
Démontrer par récurrence que , ∀n ∈ N , ∃(an ; bn)∈ N^2,
{(1 + racine(2))^n = an + bn*racine(2)
{an^2 - 2*bn^2 = ( -1)^n
j'ai commencé par mettre an + bn*racine(2) au carré et ça ma donné an^2 + 2*bn^2 , je sais pas si y'a un lien avec an^2 - 2*bn^2 = ( -1)^n , par ce que la on a une soustration ...?
Raisonnement par récurrence
7 messages
- Page 1 sur 1
Re: Raisonnement par récurrence
.
autre méthode , commencer tout de suite la récurrence:
multiplie les deux membres de l'égalité (*) par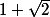
qu'est ce que ça donne ?
JeSuisNulEnMathss a écrit:L'exercice :
Démontrer par récurrence que , ∀n ∈ N , ∃(an ; bn)∈ N^2,
{(1 + racine(2))^n = an + bn*racine(2) (*)
{an^2 - 2*bn^2 = ( -1)^n (**)
autre méthode , commencer tout de suite la récurrence:
multiplie les deux membres de l'égalité (*) par
qu'est ce que ça donne ?
Modifié en dernier par mathelot le 15 Déc 2020, 21:17, modifié 2 fois.
Re: Raisonnement par récurrence
.
Modifié en dernier par mathelot le 15 Déc 2020, 16:32, modifié 2 fois.
Re: Raisonnement par récurrence
comme ça ?
(an + 2bn)^2
(an - 2bn)^2
mais après je ne sais pas quoi faire de ça ... , je ne comprend pas ou je dois aller avec ce résultat . Surtout que ça ne ressemble pas vraiment au modèle d'un raisonnement par récurrence
, je ne comprend pas ou je dois aller avec ce résultat . Surtout que ça ne ressemble pas vraiment au modèle d'un raisonnement par récurrence
(an + 2bn)^2
(an - 2bn)^2
mais après je ne sais pas quoi faire de ça ...
 , je ne comprend pas ou je dois aller avec ce résultat . Surtout que ça ne ressemble pas vraiment au modèle d'un raisonnement par récurrence
, je ne comprend pas ou je dois aller avec ce résultat . Surtout que ça ne ressemble pas vraiment au modèle d'un raisonnement par récurrenceRe: Raisonnement par récurrence
On appelle 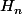 l'hypothèse de récurrence suivante:
l'hypothèse de récurrence suivante:
 \cr<br />\exists (a_n;b_n) \in \mathbb{N}^2 \cr<br />\left\{<br />\begin{array}{ccc}<br />(1 + \sqrt{2})^n &=& a_n + b_n \sqrt{2} \cr<br />a_n^2 - 2 b_n^2 &=& ( -1)^n<br />\end{array}<br />\right.)
multiplions la 1ère égalité par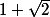 . Qu'obtenons nous ?
. Qu'obtenons nous ?
multiplions la 1ère égalité par
Re: Raisonnement par récurrence
mathelot a écrit:On appellel'hypothèse de récurrence suivante:
multiplions la 1ère égalité par. Qu'obtenons nous ?
on obtient
soit
on pose donc
que reste-t-il à vérifier ?
Re: Raisonnement par récurrence
on vérifie que
de plus
Le système
Le système
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
