Salut
J'ai cet question
Soit A un sous espace vectoriel d'un espace vectoriel E
Montrer que si A est convexe alors A+A=2A et si c'est vrai pour l'inverse?
J'ai commencé par supposer que A est convexe
Et j'ai pris x ∈ A+A <=> ∃ y∈ A et∃ z∈ A tq x=y+z
Et comme A est convexe, ∀t ∈ [0,1]
(1-t) y+ t z ∈ A
Aprés ça j'ai esseyé pas mal d'idées mais j'ai obtenu rien .
Est ce que vous pouvez me donner une idée?
Merci .
Espace vectoriel convexe
3 messages
- Page 1 sur 1
Re: Espace vectoriel convexe
Bonjour
je suppose que vous dites
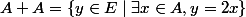
A+A est convexe six+\alpha y\in A+A)
dans ce cas Vect(2x)=Vect(x)=A=A+A et sa dimension est 1
donc le problème se résume à regarder ça sur une droite et on montre cela plus facilement (à mon avis)
je réponds car personne ne vient et aujourdhui c'est pas mon jour (j'ai dit des conneries sur un autre fil )
c'est pas pour me rattraper que je viens c'est juste parce que personne n'est venu et que bon le risque de redire une connerie deux fois le même jour est moins grand que d'en dire une seule
Edit: faute d'orthographe sur je réponds (une de moins)
je suppose que vous dites
A+A est convexe si
dans ce cas Vect(2x)=Vect(x)=A=A+A et sa dimension est 1
donc le problème se résume à regarder ça sur une droite et on montre cela plus facilement (à mon avis)
je réponds car personne ne vient et aujourdhui c'est pas mon jour (j'ai dit des conneries sur un autre fil )
c'est pas pour me rattraper que je viens c'est juste parce que personne n'est venu et que bon le risque de redire une connerie deux fois le même jour est moins grand que d'en dire une seule
Edit: faute d'orthographe sur je réponds (une de moins)
Re: Espace vectoriel convexe
Bonsoir ,pardon pour le temps mort (j'avais des autres examens)
J'ai vraiment compris ce que vous avez dire
Je sais que A+A et 2A sont des convexes
Mais j'ai pas copmris ça:
A+A convexe si
∀ x ∈ A ,∀ y ∈ A ,∀α∈[0,1] ∈ A, (1-α)x +αy ∈ A+A
Pouquoi x et y ∈ A pas dans A+A?
Et comment montrer l'inégalité j'ai pas vraiment une idée clair
Merci d'avance.
J'ai vraiment compris ce que vous avez dire
Je sais que A+A et 2A sont des convexes
Mais j'ai pas copmris ça:
A+A convexe si
∀ x ∈ A ,∀ y ∈ A ,∀α∈[0,1] ∈ A, (1-α)x +αy ∈ A+A
Pouquoi x et y ∈ A pas dans A+A?
Et comment montrer l'inégalité j'ai pas vraiment une idée clair
Merci d'avance.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
