Bonjour, j'ai cet exo à faire et je ne sais absolument pas comment m'y prendre. Pouvez-vous m'aider ?
1) Etudier le sens de variation de la suite ( un ) définie par : un = 2n² – 8n + 11 en étudiant le sens de
variation de la fonction associée à cette suite.
Merci d'avance.
Etude de variation d'une suite
9 messages
- Page 1 sur 1
Re: Etude de variation d'une suite
La "fonction associée à cette suite" est la fonction  . Tu sais certainement étudier les variations de
. Tu sais certainement étudier les variations de  .
.
Re: Etude de variation d'une suite
merci de ta réponse. J'ai trouve f'(x)=4x-8. La fonction est donc croissante.
Re: Etude de variation d'une suite
EnzoLRG a écrit:J'ai trouve f'(x)=4x-8. La fonction est donc croissante.
Cela dépend sur quel intervalle tu te places ...
Re: Etude de variation d'une suite
Sa Majesté a écrit:EnzoLRG a écrit:J'ai trouve f'(x)=4x-8. La fonction est donc croissante.
Cela dépend sur quel intervalle tu te places ...
L'intervale est de [-∞;+∞].
Re: Etude de variation d'une suite
Ah bon ? La fonction dérivée  est positive sur
est positive sur  tout entier ? Eh bien, j'en apprends tous les jours !
tout entier ? Eh bien, j'en apprends tous les jours !
Re: Etude de variation d'une suite
Bonjour,
N'hésite pas à poser un tableau de variation, ça prend 2min et tu y verras plus clair
Et après avoir poser ton tableau et trouver le sens de variation de f(x), n'oublie pas que c'est une suite, que x représente n et que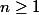 !
!
N'hésite pas à poser un tableau de variation, ça prend 2min et tu y verras plus clair
Et après avoir poser ton tableau et trouver le sens de variation de f(x), n'oublie pas que c'est une suite, que x représente n et que
Re: Etude de variation d'une suite
Sauf mention explicite du contraire, une suite ) indexée par les entiers naturels commence par
indexée par les entiers naturels commence par  .
.
Re: Etude de variation d'une suite
GaBuZoMeu a écrit:Sauf mention explicite du contraire, une suiteindexée par les entiers naturels commence par
.
En effet, erreur de ma part

9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
