Etude de variation d'une suite 1S

[maxrose]

Bonjour,
Dans un exemple, il m'est demandé de trouver le sens de variation de la suite où est donné :



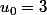
J'ai démontré en calculant qu'elle était décroissante, mais ça ne suffit pas.

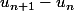
J'ai aussi tenté en calculant , et donc en trouvant la raison mais je tombe sur un calcul de fou en obtenant

.. :mur:

J'ai l'impression de m'engouffrer dans des calculs de fou, Help me, Thank's ! :lol3:

[Shew]

Bonjour,
Dans un exemple, il m'est demandé de trouver le sens de variation de la suite où est donné :



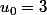
J'ai démontré en calculant qu'elle était décroissante, mais ça ne suffit pas.

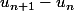
J'ai aussi tenté en calculant , et donc en trouvant la raison mais je tombe sur un calcul de fou en obtenant

.. :mur:

J'ai l'impression de m'engouffrer dans des calculs de fou, Help me, Thank's ! :lol3:

Essayez plutot

[Moicoucou]

HS : ta boite de message est pleine Shew

[Shew]

HS : ta boite de message est pleine Shew

Réglé :we:

[Shew]

Bonjour,
Dans un exemple, il m'est demandé de trouver le sens de variation de la suite où est donné :



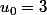
J'ai démontré en calculant qu'elle était décroissante, mais ça ne suffit pas.

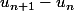
J'ai aussi tenté en calculant , et donc en trouvant la raison mais je tombe sur un calcul de fou en obtenant

.. :mur:

J'ai l'impression de m'engouffrer dans des calculs de fou, Help me, Thank's ! :lol3:

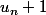
Bon pas besoin d'aller plus loin en faite, on a ensuite étudiez le signe de et de pour tout n de et répondez à la question .

[maxrose]

Ingénieux la factorisation :id:

J'ai fait ça avec le delta, et fort logiquement je trouve qu'au dessus c'est toujours positif sauf en -1.
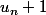
Donc j'ai aussi étudié le signe de , donc la suite est décroissante si on parvient à prouver que n'est jamais inférieur à -1.

Mais comment prouver que ? :mur:

[Shew]

Ingénieux la factorisation :id:

J'ai fait ça avec le delta, et fort logiquement je trouve qu'au dessus c'est toujours positif sauf en -1.
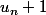
Donc j'ai aussi étudié le signe de , donc la suite est décroissante si on parvient à prouver que n'est jamais inférieur à -1.

Mais comment prouver que ? :mur:

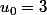
Pas besoin d'aller jusque la , pour tout n de , (le carré d'un nombre est toujours positif) et comme donc

Comme donc . Il ne vous reste plus qu'à conclure .

[maxrose]

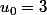
Pas besoin d'aller jusque la , pour tout n de , (le carré d'un nombre est toujours positif) et comme donc

Comme donc . Il ne vous reste plus qu'à conclure .

Parfait, c'est de ça dont j'avais besoin : , et cela me semble logique et cohérent; Merci ! :we:

[Shew]

Parfait, c'est de ça dont j'avais besoin : , et cela me semble logique et cohérent; Merci ! :we:

C'est assez logique puisque la base u0 est de 3 et le dénominateur augmente de 1 à chaque fois le précédent donc u1 + 1 > u0 et ainsi de suite :lol3:

[maxrose]

En fait, j'ai un souci avec ça; si on l'applique, on trouve que. Or ceci est faux dès le départ car

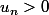
(ce qui n'empêche pas de dire que mais pourquoi à part que ça semble logique?)

Désolé de faire creuser le problème jusque là, mais j'aime bien quand les choses sont claires. Merci bien !! :we:

[Shew]

En fait, j'ai un souci avec ça; si on l'applique, on trouve que. Or ceci est faux dès le départ car

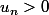
(ce qui n'empêche pas de dire que mais pourquoi à part que ça semble logique?)

Désolé de faire creuser le problème jusque là, mais j'aime bien quand les choses sont claires. Merci bien !! :we:

Oui en effet sans doute pas pour tout n . Il faudrait creuser le raisonnement je pense .

[Joker62]

Hello,

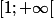
La fonction est croissante sur . Donc :

- On calcule u_1 et on le compare à u_0.

A priori ici, on a :

Ainsi :
Comme f croissante sur R+ :



Or f(1) = 1. Comme f croissante :



De proche en proche

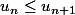
Quand la fonction associée à une suite récurrente est croissante, la suite est monotone et il suffit donc de connaitre le signe de u_1 - u_0

[Shew]

Hello,

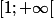
La fonction est croissante sur . Donc :

- On calcule u_1 et on le compare à u_0.

A priori ici, on a :

Ainsi :
Comme f croissante sur R+ :



Or f(1) = 1. Comme f croissante :



De proche en proche

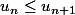
Quand la fonction associée à une suite récurrente est croissante, la suite est monotone et il suffit donc de connaitre le signe de u_1 - u_0

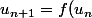C'est vrai qu'on a la relation mais comme f est croissante et il n'y a pas de relation direct entre f et

[Joker62]

Ah je me suis trompé dans mes inégalités !!! :mur:

Chaque donc est à justifier par : f croissante sur [1;+\infty[

donc donc

[Shew]

Ah je me suis trompé dans mes inégalités !!! :mur:

Chaque donc est à justifier par : f croissante sur [1;+\infty[

donc donc

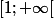
Enfin de compte on obtient la même chose en utilisant ceci en partant du principe que puisque f est croissante sur donc

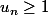
[Joker62]

Yeap,

L'idée est de voir que l'intervalle [1;+;)[ est stable par f. C'est à dire que pour tout x dans [1;+;)[, on a f(x) >= 1

Comme f est croissante sur tout ]-1;+;)[, il suffit de voir que f(1) = 1 et c'est fini.

[Shew]

Yeap,

L'idée est de voir que l'intervalle [1;+;)[ est stable par f. C'est à dire que pour tout x dans [1;+;)[, on a f(x) >= 1

Comme f est croissante sur tout ]-1;+;)[, il suffit de voir que f(1) = 1 et c'est fini.

Merci pour l'idée, ça peut toujours me servir :we: