Comparaison de nombres
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Lilirose
- Membre Naturel
- Messages: 47
- Enregistré le: 06 Sep 2006, 14:12
-
 par Lilirose » 28 Nov 2006, 19:15
par Lilirose » 28 Nov 2006, 19:15
Bonsoir! Je bloque sur ce cas: (on vient juste de faire cela en classe)
Comparer A et B en étudiant le signe de leur différence :
A-B= (x+5)² - (25+10x)
A-B=(x-5)²-(x+5)²
A-B= [(x-5+x+5)] [(x-5-x-5)]
A-B= -20x
Et après je suis bloquée ...
Merci de m'aider!
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 28 Nov 2006, 19:29
par rene38 » 28 Nov 2006, 19:29
Bonjour
A-B= (x+5)² - (25+10x)
A-B=(x-5)²-(x+5)²
Comment passes-tu de la première ligne à la deuxième ?
-
Lilirose
- Membre Naturel
- Messages: 47
- Enregistré le: 06 Sep 2006, 14:12
-
 par Lilirose » 29 Nov 2006, 10:44
par Lilirose » 29 Nov 2006, 10:44
Ah oui en effet je me suis trompée... il faut développer alors?
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 29 Nov 2006, 10:45
par Elsa_toup » 29 Nov 2006, 10:45
Oui il faut que tu développes le tout.
-
Lilirose
- Membre Naturel
- Messages: 47
- Enregistré le: 06 Sep 2006, 14:12
-
 par Lilirose » 29 Nov 2006, 11:05
par Lilirose » 29 Nov 2006, 11:05
D'accord.
A-B= (x+5)²-25+10x
A-B=x²+10x+25-(25+10x)
A-B=x²+10x+25-25-10x
A-B=x²
Pour tout réel x, x²>0, donc a-b>0 d'où a>B
C'est bon?
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 29 Nov 2006, 11:08
par Elsa_toup » 29 Nov 2006, 11:08
Tout à fait. Petite remarque cependant : à moins qu'il te soit dit que x
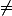
0, les inégalités sont larges...
-
Lilirose
- Membre Naturel
- Messages: 47
- Enregistré le: 06 Sep 2006, 14:12
-
 par Lilirose » 29 Nov 2006, 11:14
par Lilirose » 29 Nov 2006, 11:14
Comment ça?
Sinon merci beaucoup de m'aider Elsa_toup :happy2:
-
maturin
- Membre Irrationnel
- Messages: 1193
- Enregistré le: 09 Nov 2006, 16:28
-
 par maturin » 29 Nov 2006, 11:23
par maturin » 29 Nov 2006, 11:23
ben tu as

et non x²>0
car x²=0 si x=0.
donc

et non A>B
-
Lilirose
- Membre Naturel
- Messages: 47
- Enregistré le: 06 Sep 2006, 14:12
-
 par Lilirose » 29 Nov 2006, 11:31
par Lilirose » 29 Nov 2006, 11:31
Ah d'accord je vois! Non, il est bien precisé que x désigne un réel non nul =)
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 29 Nov 2006, 11:41
par Elsa_toup » 29 Nov 2006, 11:41
Bon alors pas la peine....
Tes inégalités sont donc correctes ! :happy2:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
