Congruence

[Theo2732]

Quelqu’un sait comment faire ?
Un magicien et son assistant performant un tour de magie:

Tout d’abord, le magicien se fait enfermer par son assistant, de sorte qu’il ne puisse rien voir ou entendre. Ensuite, l’assistant invite un membre de l’audience et lui demande de placer une pièce sur chaque case d’un echéquier n x n, soit sur pile, soit sur face. De plus, il lui demande d’indiquer une case C de l’échiquier. L’assistant choisit alors une case (pas nécessairement la même) et retourne la pièce située dessus. Finalement, l’assistant libère le magicien qui, à la seule vue de l’échiquier, devine la case C.

[GaBuZoMeu]

Le titre "congruence" indique dans quelle direction rechercher.
Quelle information est importante ? la position de la case C. Il y a positions possibles pour cette case. Cette information peut être portée par un entier modulo , en numérotant les cases de 0 à .
Comment trouver une fonction qui associe à une configuration des pièces sur l'échiquier un entier modulo , de telle façon que l'assistant, en retournant une seule de ces pièces, puisse toujours arriver à une configuration dont l'image est l'entier modulo qui est le n° de la case C ?

[Ben314]

Salut,
Perso., je sais pas trop comment procéder en utilisant des congruences.
Par contre je sais faire en utilisant l'opérateur "ou exclusif binaire" (*) :


(*) Qui correspond à la différence symétrique sur l'ensemble des parties d'un ensemble donné.

[Theo2732]

C’est bon j’ai trouvé avec l’opérateur bigoplus et une analyse synthèse...
merci

[GaBuZoMeu]

Je suis perplexe.
Je n'arrive pas à faire marcher la voie que j'indiquais, en utilisant les congruences.
Je reprends la situation.
On numérote les cases de l'échiquier de à
Les configurations de l'échiquier avec les pièces sont codées par les éléments de (0 pour pile, 1 pour face), qu'on peut voir comme espace vectoriel de dimension sur le corps à deux éléments. Je note la base canonique de cet espace vectoriel (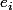 est le vecteur dont toutes les composantes sont sauf la -ème qui est ).
On doit associer à chacune de ces configurations, c.-à-d. à chaque élément de une case, c.-à-d. un élément de 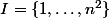. On veut une fonction (la fonction qui permet au magicien de trouver la bonne case) et on veut que cette fonction satisfasse la propriété suivante :

(c'est la propriété qui permet à l'assistant du magicien, quelles que soient la configuration et la case choisies par le membre de l'audience, de pouvoir modifier sur une seule case de façon à ce que le magicien trouve bien le numéro à partir de la configuration modifiée). À noter que ce est en fait unique, c'est une fonction de et .

J'ai pris la peine de formaliser mathématiquement le problème de façon la plus explicite possible. Et arrivé là, je ne vois pas comment le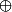 de Ben314 (qui correspond, si j'ai bien compris, à l'addition dans l'espace vectoriel sur le corps à deux éléments) permet de trouver une fonction qui remplit le cahier des charges. Je dois dire que je n'arrive pas non plus à m'en sortir avec la congruence modulo . A priori, le fait que le nombre de cases soit un carré ne me semble pas crucial, et je dirais qu'on peut remplacer par n'importe quel entier .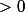

Il y a sans doute quelque chose d'évident que je ne vois pas. Bref, j'aimerais des explications.

[GaBuZoMeu]

Un exemple de fonction satisfaisant le cahier des charges pour le cas :

Code: Tout sélectionner

0000     4
0001     1
0010     2
0100     3
1000     4
0011     3
0101     1
0110     2
1001     2
1010     1
1100     3
0111     4
1011     3
1101     2
1110     1
1111     4

Ce n'est pas glorieux, et je n'arrive pas à en tirer quelque chose de général.

[Ben314]

Le "tour de magie"en question est relativement connu et ça fait plusieurs fois que je le rencontre (il doit en particulier y avoir déjà un ou deux thread du forum qui en traitent) donc je parle plus de mémoire qu'en ayant réellement (re)fait tout les raisonnements.

Bref, sauf erreur, pour un ensemble fini , si on cherche une application telle que
alors une telle application n'existe que si le cardinal de est une puissance de 2 et dans ce cas, elle est unique à isomorphisme prés sur l'e.v. de départ.
Et l'application en question c'est le "ou exclusif en base 2" des indices tels que lorsque .

[GaBuZoMeu]

Depuis le début, cette histoire me fait fortement penser aux codes correcteurs d'erreur. Et la théorie des codes correcteurs d'erreur donne une solution (une fonction satisfaisant le cahier des charges détaillé plus haut), au moins dans le cas où est une puissance de , disons .
Alors on peut utiliser un code de Hamming de la manière suivante.

Une configuration de l'échiquier est codée par un vecteur binaire (écrit en ligne) de longueur .

Soit la matrice de taille dont les vecteurs lignes sont les écriture binaires, sur bits, des entiers de à . Si est un tel entier, je note cette écriture binaire vue comme vecteur de longueur sur le corps à deux éléments. La -ème ligne de est .

Le syndrome d'une configuration de l'échiquier est l'entier entre et tel que l'écriture binaire de 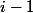est (le calcul matriciel se fait bien sûr sur le corps à deux éléments). Autrement dit, .

Partant d'une configuration donnée et d'un entier entre et , il existe un unique entier entre et tel que la configuration (obtenue en modifiant la configuration uniquement sur la case n° ) ait pour syndrome . En effet, on veut

et ceci équivaut à .

La fonction "syndrome" fournit donc une fonction satisfaisant au cahier des charges. La terminologie "syndrome" vient de la théorie des codes correcteurs, et la matrice est à un chouïa près la matrice de contrôle d'un code de Hamming binaire.

Je me demande
1°) si ça peut s'étendre à des tailles qui ne sont pas des puissances de 2,
2°) si ça correspond à ce à quoi pensait Ben314. Sinon, à quoi pensait-il ? Je suis curieux de l'apprendre.

PS. Le temps d'écrire ce long message, Ben314 a posté une réponse. C'est bien ce à quoi il pensait, et on n'a pas de réponse en dehors des tailles qui sont des puissances de 2.

[GaBuZoMeu]

Je reviens sur cette affirmation de Ben314

Bref, sauf erreur, pour un ensemble fini , si on cherche une application telle que
alors une telle application n'existe que si le cardinal de est une puissance de 2 et dans ce cas, elle est unique à isomorphisme prés sur l'e.v. de départ.

Il n'est pas très difficile de donner une démonstration du premier point : il est nécessaire que le cardinal de , disons , soit une puissance de 2.
Sur il y a une distance bien connue en théorie des codes correcteurs : la distance de Hamming. La distance de Hamming entre deux mots binaires de longueur N est le nombre de bits sur lesquels ils différent. Par exemple la distance de Hamming entre 110100010 et 100100100 est 3.
La condition posée sur la fonction peut se reformuler ainsi : pour toute sphère de Hamming de rayon 1 dans et tout 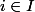, il existe un et un seul tel que . Supposons ; sous cette hypothèse le centre d'une centre de Hamming de rayon 1 est uniquement déterminé (il est déterminé par trois points sur la sphère). Il y a donc 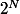sphères de Hamming de rayon 1 et par chaque passent sphères de Hamming de rayon 1. Pour chaque 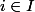, le nombre de tels que est par conséquent égal à , ce qui prouve que divise 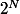et est donc une puissance de 2.

Venons-en maintenant au deuxième point : l'unicité de à composition avec un isomorphisme linéaire de l'espace de départ près. Là, ça me semble faux.
L'application construite dans le message ci-dessus (le syndrome) a la propriété que les sont des sous-espaces affines parallèles dans . Ça reste bien sûr vrai si on compose avec un isomorphisme linéaire de l'espace vectoriel de départ. Or ce n'est clairement pas vrai du que j'ai donné explicitement pour le cas 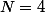. D'accord, Ben ?

[Ben314]

Effectivement : après quelques essais, il me semble bien que la solution que tu expose ne soit pas de la forme que j'ai mentionné dans mon précédent post.
Donc on peut éventuellement chercher combien il existe de fonctions solutions du problème et éventuellement de quelle forme elles sont.

[Mateo_13]

Bonjour Ben314 et GaBuZoMeu,

désolé si je suis hors-sujet,
mais l'énoncé initial me rappelle un autre semblable,
mais je ne sais pas si cela peut vous donner des idées pour celui qui vous intéresse :
https://youtu.be/OXz64qCjZ6k

Amicalement,
--
Mateo.

[GaBuZoMeu]

Bonjour Ben,

Quand tu parles de "la solution que tu exposes", tu veux dire celle décrite pour pour le cas 2x2 par la donnée de la fonction ?
Parce que dans le long message que j'ai posté après, je décris en détail la solution basée sur les codes de Hamming qui marche pour les tailles qui sont une puissance de 2, et ça correspond à celle que tu as mentionnée (sauf que tu as peut-être un problème de décalage de 1 : tu comptes les indices à partir de 0 ?

Bonjour Mateo,

La vidéo que tu as mise en lien concerne aussi un "tour de magie" basé sur la théorie des codes correcteurs d'erreur. Dans le cas de cette vidéo il s'agit d'un code très simple, qui consiste à simplement ajouter un bit de parité (ce qui permet de détecter une erreur). L'ajout d'un bit de parité à chaque ligne et chaque colonne permet de trouver la ligne et la colonne en erreur, donc la case retournée.

Le code de Hamming utilisé dans le tour objet du présent fil est plus évolué. On peut le retrouver dans le "tour" expliqué dans cette page d'"Images de Mathématiques". Ce tour consiste à deviner un smiley parmi 16 en posant sept questions à réponse oui ou non, avec la possibilité pour le répondeur de mentir au plus une fois ; il repose sur la capacité du code de Hamming (ici le code de Hamming (7,4,3)) à corriger une erreur.