Hello quelqu’un sait comment faire ça ?
Déterminer tous les entiers positifs “n” pour lesquels il existe un entier “a” tel que (2^n)-1 divise (a^2) +9.
Merci à tous
Congruence
8 messages
- Page 1 sur 1
Re: Congruence
Je n'ai pas cherché mais l'énoncé est équivalent a -9 est reste quadratique modulo 2^n-1 .
Donc symbole de Legendre ouJacobi pour piste ?
Donc symbole de Legendre ouJacobi pour piste ?
Re: Congruence
Merci beaucoup je vois toujours pas vraiment comment faire. Si tu as le temps de m’expliquer...merci
Re: Congruence
Demandons à SageMath quels sont les entiers n<200 tels que -9 soit un carré modulo 2^n-1 :
Bizarre. Est-ce que ça marche encore pour 256 ?
Et si on essaie un autre entier que -9 ?
-9 a l'air bien spécial, et on a envie de formuler une conjecture à son sujet.
Yapuka démontrer la conjecture.
- Code: Tout sélectionner
[n for n in range(1,200) if Mod(-9,2**n-1).is_square()]
Bizarre. Est-ce que ça marche encore pour 256 ?
- Code: Tout sélectionner
Mod(-9,2**256-1).is_square()
Et si on essaie un autre entier que -9 ?
- Code: Tout sélectionner
[n for n in range(1,200) if Mod(5,2**n-1).is_square()]
-9 a l'air bien spécial, et on a envie de formuler une conjecture à son sujet.
Yapuka démontrer la conjecture.
Re: Congruence
Salut,
Si n'est pas une puissance de 2 alors il est divisible par un entier impair
n'est pas une puissance de 2 alors il est divisible par un entier impair  et
et 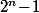 est divisible par
est divisible par  . Comme
. Comme  il est divisible par (au moins) un nombre premier
il est divisible par (au moins) un nombre premier  avec
avec  car
car  est impair.
est impair.
Pour un tel l'entier 9 est un carré inversible modulo
l'entier 9 est un carré inversible modulo  mais -1 n'est pas un carré donc -9 n'est pas un carré modulo
mais -1 n'est pas un carré donc -9 n'est pas un carré modulo  et ce n'est donc pas un carré modulo
et ce n'est donc pas un carré modulo 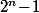 .
.
Si avec
avec  alors, pour
alors, pour  et
et 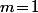 , l'entier -9 est bien un carré modulo
, l'entier -9 est bien un carré modulo 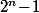 puis, vu que
puis, vu que \big(2^{2^m}\!\!+\!1\big)) où les deux facteurs sont premiers entre eux, pour montrer par récurrence que -9 est un carré modulo
où les deux facteurs sont premiers entre eux, pour montrer par récurrence que -9 est un carré modulo  il suffit de montrer que, pour
il suffit de montrer que, pour 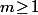 , c'est un carré modulo
, c'est un carré modulo  c'est à dire que -1 est un carré modulo
c'est à dire que -1 est un carré modulo 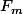 vu que 9 est un carré inversible modulo
vu que 9 est un carré inversible modulo 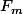 .
.
Et c'est clairement le cas vu que et que
et que ^2) .
.
Si
Pour un tel
Si
Et c'est clairement le cas vu que
Modifié en dernier par Ben314 le 28 Mar 2020, 13:50, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Congruence
Relis avec attention ce que Ben314 a écrit. Tu peux aussi avoir l'idée des solutions en relisant ce que j'ai écrit.
Re: Congruence
Parceque moi j’ai trouvé que les solutions à l’aide d’exel étaient:
Soit n=1 et donc a appartient à Z
Soit n=2 et a=3k, k appartient à Z
Soir n=4 et à=3k, k appartient à Z
Soit n=1 et donc a appartient à Z
Soit n=2 et a=3k, k appartient à Z
Soir n=4 et à=3k, k appartient à Z
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
