Bonjour,
Je dois montrer qu'une variable aléatoire à densité Tn admet une espérance. Pour se faire je dois montrer que l'intégrale de moins l'infini à plus l'infini de x * f(x) dx converge absolument si je ne me trompe.
La densité étant nulle sur moins l'infini - 0, je dois montrer que l'intégrale de 0 à + l'infini de x*f(x) dx converge absolument. Le soucis étant que je ne vois pas comment établir ceci.
Je dois donc montrer que l'intégrale de 0 à + l'infini défini par : x*(n*exp(-x)*(1-exp(-x))^n-1) dx converge absolument.
Pouvez-vous m'aider svp, merci d'avance.
Convergence d'une intégrale
4 messages
- Page 1 sur 1
Re: Convergence d'une intégrale
Tu ne nous as pas présenté  . Je suppose que c'est
. Je suppose que c'est ^{n-1}) sur
sur  ?
?
Tu peux utiliser la croissance comparée de l'exponentielle et des puissances de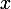 pour montrer que ton intégrale est bien convergente en
pour montrer que ton intégrale est bien convergente en 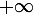 , en comparant par exemple à ... quelque chose dont tu sais que l'intégrale est convergente en
, en comparant par exemple à ... quelque chose dont tu sais que l'intégrale est convergente en 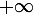 .
.
Tu peux utiliser la croissance comparée de l'exponentielle et des puissances de
Re: Convergence d'une intégrale
Oui pardon, sa densité est bien définie par cette expression et par 0 sur moins l'infini - 0!
D'accord je prends note je vais tenter de faire par ce moyen. Merci pour votre message !
D'accord je prends note je vais tenter de faire par ce moyen. Merci pour votre message !
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
