Bonjour j'ai un exercice de maths et je n'y arrive pas.
Pour tout réel k, on définit la fonction numérique Fk de la variable réelle x par: Fk(x)= 3x^2+kx+3/x^2 + 1.
On note Ck sa courbe représentative dans un repère orthogonal.
1)Justifier que pour tout réel k, la fonction Fk est définie sur R.
2)a)Justifier que pour tout réel k, la courbe Ck passe par le point I(0;3).
b)Justifier que pour tout réel k, la droite d'équation y=3 est une asymptote à Ck en -infinie et en +infinie.
3)Démontrer que pour tout réel k, F-k(x)=Fk(-x).Qu'en déduit-on pour les courbes Ck et C-k?
4)Justifier que plus K est grand plus Fk(1) est grand.
J'espère que vous aurez la gentillesse de m'aider.
Merci d'avance!
Fonction numérique
5 messages
- Page 1 sur 1
Re: fonction numérique
Bonjour,
Il te faudrait revoir les règles de priorité !
Fk(x)= 3x^2+kx+3/x^2 + 1 n'est pas la bonne formulation de F mais sans douteFk(x)= (3x^2+kx+3)/(x^2 + 1) ou mieux= \dfrac{3x^2+kx+3}{x^2 + 1})
Pour t'aider il faudrait savoir où tu en es dans cet exercice ...
1) F_k(0) ne dépend pas de k
2-b) Quelle est le limite de}{x^2}) en
en 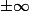 ?
?
L'infini ne prend pas de e final !
Il te faudrait revoir les règles de priorité !
Fk(x)= 3x^2+kx+3/x^2 + 1 n'est pas la bonne formulation de F mais sans douteFk(x)= (3x^2+kx+3)/(x^2 + 1) ou mieux
Pour t'aider il faudrait savoir où tu en es dans cet exercice ...
1) F_k(0) ne dépend pas de k
2-b) Quelle est le limite de
-infinie et en +infinie.
L'infini ne prend pas de e final !
Re: fonction numérique
mcfit a écrit:Comment on fait pour démontrer la question 1?
F_k est un quotient de deux polynômes. Le dénominateur ne s'annule pas. F_k est donc définie sur
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
