Domaine de définition

[Andriamoi]

Bonjour j'ai eu un contrôle aujourd'hui et je n'ai rien écrit. Je ne savais pas quoi écrit. Si vous pouvez m'aidez s'il vous plaît. Voici la question :

On nous demande en premier le tableau de variation de la fonction sur [0,pi]:
F(x) = exp(sin(2x))

Dans ma tête c'était, d'abord faire la dérivé, f'(x). Ce qui m'a donner = 2 cos(2x)exp(sin(2x)). Je me dis donc que tt ce qui est devant le exp vont s'annuler... Et on sait que l'exp ne s'annule pas.. Et la je beugue.

J'ai ainsi, exp (sin(2x)) =0 or je me suis dit on a 0 = pi/2....mais ça ne m'enlève pas l'exp et encore moins me donne un Df...

Est quelqu'un à une idée à me proposer ?
Mercii.

[mathelot]

bonjour,
l'exponentielle ne s'annule pas et reste strictement positive. Le signe de la dérivée f' de la fonction f est le signe de cos(2x).

cos(2x)=0 équivaut à:



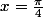
ou





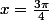
on a le tableau de signes de la dérivée:


est strictement croissante


est strictement décroissante


est strictement croissante
et le même système avec des inégalités strictes partout.

[LB2]

Bonjour,

une autre méthode :

la fonction exponentielle étant strictement croissante, et composer par une fonction strictement croissante ne changeant pas la monotonie, les variations de f sont les variations de x -> sin(2x)

et ça tu dois savoir l'étudier, soit en dérivant (et ou retrouve le signe de cos(2x)), soit en te ramenant avec le changement de variable y=2x à la fonction usuelle y-> sin(y)

[Andriamoi]

Oh Mercii beaucoup à vous ! Je n'avais pas du tt compris le sujet et ces méthode ne m'ont même pas passé par là tête ...


Mercii encore.

[mathelot]

effectivement tu as beugué en écrivant une assertion (exp(x)>0) puis son contraire (exp(x)=0)
à l'avenir, si tu es dans la même situation, soupèse chaque assertion et choisis une assertion plutôt que l'autre.