Bonsoir,
Désolé pour le post tardif mais j’ai passé trop de temps sur cette équation
z^2 + (2i-1)z - 1 - i = 0
J’ai cherché des méthodes de résolution et ai regardé des exemples s’en rapprochant sur Exo7 mais rien n’y fait mes z1 et z2 ne sont pas bons.
Je pense me tromper sur mes a,b et c.
a=1
b=(2i - 1)
c=(-1 - i) (ou 1 - i ???)
Avec ceci on obtient Delta=1, et en utilisant z1= (-b + 1)/2a et z2= (-b - 1)/2a j’obtiens z1= - i + 1 et z2= -i, tout cela semble correct mais en remplaçant dans l’équation rien ne fonctionne
Je sors d’une période difficile et j’ai accumulé pas mal de retard, merci et bonne soirée à tous.
Équation complexe
11 messages
- Page 1 sur 1
Re: Équation complexe
Si je prends les solutions que j’ai trouvé et que je remplace z par ces dernières dans mon équation je suis censé trouver 0 ? Quand j’essaye avec z1 cela semble fonctionner mais avec z2 non..
merci de votre réponse
merci de votre réponse
Re: Équation complexe
D’accord donc j’ai tourné en rond parce que je faisais (-i^2) au lieu de (-i)^2...
Merci d’avoir pris le temps de répondre,
Bonne soirée
Merci d’avoir pris le temps de répondre,
Bonne soirée
Re: Équation complexe
Re ! Désolé pour le up
J’ai mis mes solutions sous forme trigonométrique:
z1=sqrt(2)(cos(3pi/4)+i.sin(3pi/4)
z2=(cos(3pi/2)+i.sin(3pi/2)
On me demande d’en déduire les solutions sous forme trigonométrique de z^6 + (2i-1)z^3 - 1 - i=0
Je dois mettre mes solutions au cube ?
Merci pour votre lecture
J’ai mis mes solutions sous forme trigonométrique:
z1=sqrt(2)(cos(3pi/4)+i.sin(3pi/4)
z2=(cos(3pi/2)+i.sin(3pi/2)
On me demande d’en déduire les solutions sous forme trigonométrique de z^6 + (2i-1)z^3 - 1 - i=0
Je dois mettre mes solutions au cube ?
Merci pour votre lecture
Re: Équation complexe
Réfléchis :  est solution de
est solution de z^3 - 1 - i=0) si et seulement si
si et seulement si 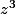 est solution de
est solution de z - 1 - i=0) .
.
Es-tu sûr qu'élever au cube les solutions de la deuxième équation soit la bonne manip à faire ?
Es-tu sûr qu'élever au cube les solutions de la deuxième équation soit la bonne manip à faire ?
Re: Équation complexe
Je dois passer par la forme exponentielle et résoudre ?
Le soucis c’est Que je dois les déduire sous forme trigonométrique et honnêtement je ne sais pas trop comment y faire..
je sais que j’aurai 6 solutions
Le soucis c’est Que je dois les déduire sous forme trigonométrique et honnêtement je ne sais pas trop comment y faire..
je sais que j’aurai 6 solutions
Re: Équation complexe
Bon, tu n'as pas capté. 
Autrement dit, si et seulement si ou
ou  , où
, où  sont les deux solutions que tu as trouvées pour l'équation du second degré. Vois-tu maintenant l'intérêt de les avoir sous forme trigonométrique ?
sont les deux solutions que tu as trouvées pour l'équation du second degré. Vois-tu maintenant l'intérêt de les avoir sous forme trigonométrique ?

GaBuZoMeu a écrit:si et seulement siest solution de
.
Autrement dit, si et seulement si
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
