Inéquation

[Wings2016]

Bonsoir
Comment je dois faire pour résoudre cette inéquation enfin j'ai essayé mais je reste bloqué sur un point.
Racine(x-1)>=x-4

[Sa Majesté]

Salut
Déjà il faut que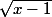 existe, ce qui signifie ...
Ensuite tu élèves au carré et tu résous l'inéquation

[Wings2016]

Oui il est défini si x>=1 . Mais si 1<x<4 on a x-4 sera négatif est ce que je pourrais élever le carré dans ce cas sans problème ???

[lyceen95]

Si x est compris entre 1 et 4, 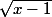est un nombre positif, et 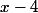est un nombre négatif (ou nul), donc tout va bien, un nombre positif est forcément supérieur ou égal à un nombre négatif.
Donc tout l'intervalle [1,4] est bien solution de notre inéquation.

Reste à traiter les cas où x > 4.

[capitaine nuggets]

Salut !



Cette inéquation est définie si et seulement si , donc le domaine de définition est ...

Ensuite, pour résoudre cette inéquation, il faut distingué deux cas suivant le signe du membre de droite :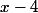 (le but étant finalement d'appliquer la propriété : si et sont deux réels tels que alors ).

1. Si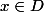 alors biensûr , mais si de plus on a , alors 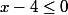, donc qu'en déduis-tu pour les réels 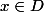tels que ?

2. Pour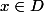 et 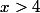, on a donc on peut appliquer la propriété que j'ai cité plus haut : en élevant chaque membre au carré, on a , ce qui équivaut à ...

Je te laisse réfléchir.

P.S. : Niveau collège et primaire !?