Parmi les ensembles suivants, reconnaître ceux qui sont des sous-espaces vectoriels :
(x, y, z) ∈ R^3 | x + y = 0
Je sais comment demontrer que 'est un S.E.V mais le "z" me pose probléme puisque il n'est pas dans x+y=0 il n'y'a aucune information sur lui
Comment dois-je m'y prendre?
Espace vectoriel
9 messages
- Page 1 sur 1
Re: Espace vectoriel
Pourquoi l'absence du  te fait-elle peur ?
te fait-elle peur ?
Par exemple, quelle difficulté aurais-tu à montrer que, si\in F) et
et \in F) , alors
, alors \in F) (où
(où  est le sous-ensemble de
est le sous-ensemble de 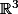 qui t'es donné) ?
qui t'es donné) ?
Par exemple, quelle difficulté aurais-tu à montrer que, si
Re: Espace vectoriel
donc les composantes du vecteur non pas d'importance il suffit juste de demontrer que le 0 de l'espae vectoriel appartient au S.E.V et de verifier la loi interne et externe ?
Re: Espace vectoriel
Je ne comprends pas ce que tu écris.
Reprenons calmement. Pour montrer que est un sous-espace vectoriel de
est un sous-espace vectoriel de 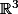 , qu'as-tu à montrer ? Essaie de répondre clairement et précisément.
, qu'as-tu à montrer ? Essaie de répondre clairement et précisément.
Reprenons calmement. Pour montrer que
Re: Espace vectoriel
Pour démontrer que c'est un sous espace vectoriel je m'y suis prise comme suis:
0+0=0 implique que 0 de R^3 ∈ F
et que :
∀ u (x,y,z)∊ F / x+y=0
∀ v (x',y',z') ∊ F / x'+y'=0
∀ (α,β)∊ R^2
αu+βv= α (x,y,z) +β (x',y',z')= (αx+βx' , αy+βy')
on pose :
αx+βx'=X et αy+βy' =Y
X+Y= αx+βx +αy+βy' = α(x+y) +β(x'+y') = 0
Donc c'est un S.E.V
0+0=0 implique que 0 de R^3 ∈ F
et que :
∀ u (x,y,z)∊ F / x+y=0
∀ v (x',y',z') ∊ F / x'+y'=0
∀ (α,β)∊ R^2
αu+βv= α (x,y,z) +β (x',y',z')= (αx+βx' , αy+βy')
on pose :
αx+βx'=X et αy+βy' =Y
X+Y= αx+βx +αy+βy' = α(x+y) +β(x'+y') = 0
Donc c'est un S.E.V
Re: Espace vectoriel
OK, sauf ça :
Peux-tu corriger ?
meriemar a écrit:αu+βv= α (x,y,z) +β (x',y',z')= (αx+βx' , αy+βy')
Peux-tu corriger ?
Re: Espace vectoriel
J'ai oublié le "z" je me suis focaliser le x et le y 
αu+βv= α (x,y,z) +β (x',y',z')= (αx+βx' , αy+βy', αz+βz')
on pose :
αx+βx'=X et αy+βy' =Y
X+Y= αx+βx +αy+βy' = α(x+y) +β(x'+y') = 0
Donc c'est un S.E.V
c'est correct maintenant ?

αu+βv= α (x,y,z) +β (x',y',z')= (αx+βx' , αy+βy', αz+βz')
on pose :
αx+βx'=X et αy+βy' =Y
X+Y= αx+βx +αy+βy' = α(x+y) +β(x'+y') = 0
Donc c'est un S.E.V
c'est correct maintenant ?
Re: Espace vectoriel
Oui, à la rédaction près qui peut être un peu améliorée.
Un exemple tout bête : écrire "Donc F est un sous-espace vectoriel" au lieu de "Donc c'est un sous-espace vectoriel", ne prend pas plus de place, et est beaucoup plus précis.
Un exemple tout bête : écrire "Donc F est un sous-espace vectoriel" au lieu de "Donc c'est un sous-espace vectoriel", ne prend pas plus de place, et est beaucoup plus précis.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 92 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
