n' admet pas de solutions dans
Congruence
12 messages
- Page 1 sur 1
Re: congruence
c'est aussi chercher k entier relatif tel que
x²+1=3+4k
soit
x² =3-1+4k
x²=2-4k
met 2 en facteur et réfléchi comment sont les facteurs premier d'un nombre de la forme x²
x²+1=3+4k
soit
x² =3-1+4k
x²=2-4k
met 2 en facteur et réfléchi comment sont les facteurs premier d'un nombre de la forme x²
Re: congruence
pascal16 a écrit:c'est aussi chercher k entier relatif tel que
x²+1=3+4k
Non. La question posée c'est: si k est un entier tel que 3+4k est premier, existe-t-il un entier x tel que que 3+4k divise x^2+1 ?
Re: congruence
Abdelmalek n'a montré aucun signe de travail sur cette question et semble s'en être désintéressé.
@pascal16 : si on invoque le groupe multiplicatif des éléments inversibles modulo , ça te fait fuir ?
, ça te fait fuir ?
@pascal16 : si on invoque le groupe multiplicatif des éléments inversibles modulo
Re: congruence
Bonjour, la question revient à savoir si -1 est un carré dans Z/pZ, combien y a-t-il de carrés dans Z/pZ ?
Re: congruence
Bonjour
Bonjour
Faut tout de même pas pousser, parler de groupe multiplicatif modulo p alors que c'est un exercice de niveau terminale (sauf erreur de ma part, le petit th de Fermat se voit en terminale.)
@abdelmalek.2008. J'espère que tu connais ce th?
Alors on va l'utiliser: D'après le th de Fermat, on a: pour tout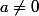 mod (p) ,
mod (p) , mod (p) .
mod (p) .
Il faut faire un raisonnement par l'absurde: dans Z/pZ
si il existe tq
tq 
alors) et
et 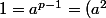^{\frac{p-1}{2}}=(-1)^{\frac{p-1}{2}})
Mais^{\frac{p-1}{2}}=1) n'est possible que si
n'est possible que si 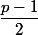 est pair.
est pair.
Or si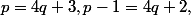 et
et /2=2q+1) est impair d'où la contradiction.
est impair d'où la contradiction.
GaBuZoMeu a écrit:@pascal16 : si on invoque le groupe multiplicatif des éléments inversibles modulo, ça te fait fuir ?
Bonjour
Faut tout de même pas pousser, parler de groupe multiplicatif modulo p alors que c'est un exercice de niveau terminale (sauf erreur de ma part, le petit th de Fermat se voit en terminale.)
@abdelmalek.2008. J'espère que tu connais ce th?
Alors on va l'utiliser: D'après le th de Fermat, on a: pour tout
Il faut faire un raisonnement par l'absurde: dans Z/pZ
si il existe
alors
Mais
Or si
Re: congruence
D'accord, c'est une preuve élémentaire (modulo le petit théorème de Fermat) que s'il y a un élément d'ordre 4 dans le groupe multiplicatif des inversibles modulo p, alors p-1 doit être divisible par 4. Bravo !
Re: congruence
aviateur a écrit:Bon maintenant on t'a débloquée avec 2 preuves, tu as le choix.
----------------
aviateur . merci beaucoup pour votre aide
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
