bonjour,
j'aimerais avoir des renseignement sur un exercice qui me pose problème
voici l'énoncé:
Soit f la fonction définie sur ]0; + infinie [ par:
f(x)= ln( x^2/x+1)
1. Déterminer les limites de f aux bornes de son ensemnle de définition.
2. Etudier les variations de la fonction f sur ]0; + infinie [
voici ma démarche pour la 1.
*lim x+1= 0+1 = 1, par contiuité des fonctions polynomes,
x tend vers 0
x superieur a 0
lim ln x= - infinie donc par compositions: lim ln ( x^2 / x+1 ) = - infinie
x tend vers 0 x tend vers 0
x superieur a 0 x superieur a 0
d'ou lim f(x) = - infinie
x tend vers 0
x superieur a 0
* lim x^2/x+1 = +∞ et lim ln x = +∞ donc lim ln ( x^2/x+1) = +∞
x tend vers +∞ x tend vers +∞ x tend vers +∞
2. je ne sais pas
merci d'avance pour votre aide
Fonction ln
5 messages
- Page 1 sur 1
Re: fonction ln
Bonjour, ton raisonnement à la question 1) est correct, juste justifie bien que  car
car  puisque tu as une forme indéterminée de la forme
puisque tu as une forme indéterminée de la forme 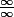 . Pour la 2) il faut étudier le signe de la dérivée en utilisant
. Pour la 2) il faut étudier le signe de la dérivée en utilisant '=\frac{u'}{u}) .
.
Re: fonction ln
Je prends u = x+1 ?
Si on dérive ça fait 1 donc 1/x+1 ? Et je fais le tableau de signe ?
Si on dérive ça fait 1 donc 1/x+1 ? Et je fais le tableau de signe ?
Re: fonction ln
Poses =\frac{x^2}{x+1}) de sorte que
de sorte que =\ln(u(x))) puis dresse le tableau de signes de f' pour en déduire le tableau de variations de f.
puis dresse le tableau de signes de f' pour en déduire le tableau de variations de f.
Re: fonction ln
ah d'accord alors voici ma corection:
j,'ai pris u= x^2
u'=2x
v=x+1
v'=1
j'utilise la formule u/v ce qui me donne aprs calcule :
u'(x)= x^2 + 2x / (x+1)2
je peux faire le tableau de signe ou je dos mettre sous forme ln (u)' = u'/u ??
j,'ai pris u= x^2
u'=2x
v=x+1
v'=1
j'utilise la formule u/v ce qui me donne aprs calcule :
u'(x)= x^2 + 2x / (x+1)2
je peux faire le tableau de signe ou je dos mettre sous forme ln (u)' = u'/u ??
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
