Bonjour,
https://math.unice.fr/~ribot/enseigneme ... sation.pdf
dans ce lien ci-dessus, j ai essayé de faire l exercice 5, j'ai réussi à faire la question 5.1 mais je n'arrive pas à faire la question suivante . J'aimerais donc avoir votre aide.
Cordialement
Un pas d armijo
7 messages
- Page 1 sur 1
Re: un pas d armijo
Bonjour
Pour simplifier je note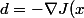) la direction de descente.
la direction de descente.
Tu peux d'abord démontrer l'inégalité
\leq J(x)+ \alpha \nabla J (x).d +\dfrac{\gamma}{2} \alpha^2 ||d||^2)
Ce qui donne
\leq J(x)+ \alpha(1- \dfrac{\gamma}{2} \alpha) \nabla J (x).d= J(x)-\alpha(1- \dfrac{\gamma}{2} \alpha)||\nabla J(x)||^2)
Donc}{\gamma}) on aura avec le choix
on aura avec le choix
 la suite
la suite 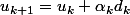 (
(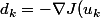) )
)
strictement décroissante.
De plus :
< J(u_k)- c ||\nabla J(x)||^2.) pour tout k.
pour tout k.
En sommant membre à membre on obtient
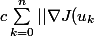||^2<J(u_1)-J(u_n))
Si la suite décroissante) ne tend pas vers
ne tend pas vers  alors elle converge .
alors elle converge .
alors l'inégalité précédente implique) tend vers 0. cqfd
tend vers 0. cqfd
Pour simplifier je note
Tu peux d'abord démontrer l'inégalité
Ce qui donne
Donc
strictement décroissante.
De plus :
En sommant membre à membre on obtient
Si la suite décroissante
alors l'inégalité précédente implique
Modifié en dernier par aviateur le 18 Avr 2019, 08:11, modifié 1 fois.
Re: un pas d armijo
Merci beaucoup pour ta réponse. Mais j ai une petite question , si la suite j(xk) décroissante et tend vers -infini est ce que la norme du gradient tend vers 0?
Re: un pas d armijo
Bonjour
Si la suite) tend vers
tend vers  il n' y a aucune raison que le gradient tende vers 0.
il n' y a aucune raison que le gradient tende vers 0.
Si la suite
Re: un pas d armijo
Donc la suite Uk vérifie lim gard (uk)=0
Et lim j (uk)=-infini n est pas vérifié? C est bien ça ?
Et lim j (uk)=-infini n est pas vérifié? C est bien ça ?
Re: un pas d armijo
Pas du tout . D'ailleurs, relie la question: la question c'est (au moins) l'une des 2 conditions est vérifiée
Je démontre que si la première n'est pas vérifiée alors on a la deuxième.
C'est équivalent à dire que l'une des 2 est vérifiée.
Je démontre que si la première n'est pas vérifiée alors on a la deuxième.
C'est équivalent à dire que l'une des 2 est vérifiée.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
