Suites
15 messages
- Page 1 sur 1
Suites
Bonjour je bloque sur un exercice de maths j‘ai sur les suites j‘ai u0= 1 et un+1= 7un+7 je dois dire à partir de quel rang n il y a un > ou = 100
J‘ai essayé d‘exprimer un à partir de un+1 mais je n‘y arrive pas j‘aurai besoin d‘aide svp merci
J‘ai essayé d‘exprimer un à partir de un+1 mais je n‘y arrive pas j‘aurai besoin d‘aide svp merci
Re: Suites
Bonjour, détermine la constante c telle que 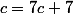 puis considère la suite de terme générale
puis considère la suite de terme générale 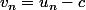 , montre qu'elle est géométrique, tu pourras en déduire sa formule explicite puis avoir l'expression explicite de
, montre qu'elle est géométrique, tu pourras en déduire sa formule explicite puis avoir l'expression explicite de  .
.
Re: Suites
J‘ai une seconde question est ce correct ? :
https://fr-static.z-dn.net/files/d7a/e2 ... 5c0c6.jpeg
https://fr-static.z-dn.net/files/d7a/e2 ... 5c0c6.jpeg
Re: Suites
J'imagine que la question c'est de donner une formule explicite de  mais en laissant du
mais en laissant du  ça peut pas être bon. Pour savoir si c'est vraiment la formule explicite, il faut te demander si tu peux directement calculer le terme de la suite sans calculs antérieurs. Je sais pas d'où tu sors cette formule mais la démarche naturelle est de remarquer que
ça peut pas être bon. Pour savoir si c'est vraiment la formule explicite, il faut te demander si tu peux directement calculer le terme de la suite sans calculs antérieurs. Je sais pas d'où tu sors cette formule mais la démarche naturelle est de remarquer que ) est une suite arithmétique donc tu peux donner une formule explicite de
est une suite arithmétique donc tu peux donner une formule explicite de  .
.
Re: Suites
Mais je ne comprends pas puisque vn étant la somme des termes de (un) la formule dit que S= nbtermes*(1er+dernier terme ) / 2
Re: Suites
Tu peux dire ça mais je préfère dire que 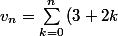=3(n+1)+2\sum_{k=0}^{n}k=3(n+1)+n(n+1)=(n+1)(n+3)) . Avec ta formule t'obtiens
. Avec ta formule t'obtiens 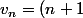\frac{3+(3+2n)}{2}=(n+1)(n+3)) , on trouve le même résultat.
, on trouve le même résultat.
Re: Suites
Et non, dans 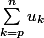 il y a
il y a 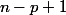 termes, prends l'exemple de la somme
termes, prends l'exemple de la somme 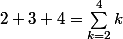 , il y a 3 termes donc dans
, il y a 3 termes donc dans  il y a n+1 termes.
il y a n+1 termes.
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
