Intersection tangente/courbe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Majaspique
- Membre Naturel
- Messages: 96
- Enregistré le: 28 Nov 2017, 22:59
-
 par Majaspique » 20 Jan 2019, 15:33
par Majaspique » 20 Jan 2019, 15:33
Bonjour,
j'ai du mal à comprendre cet exercice :
Soit

de

périodique et dérivable, et
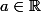
.
Montrer qu'il existe un réel

tel que la tangente en

au graphe de

coupe le graphe de

en
)) Indication : on pourra utiliser le théorème de Darboux
Indication : on pourra utiliser le théorème de DarbouxSi j'ai bien compris :
L'équation de la tangente en

s'écrit :
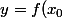 + (x-x_0)f'(x_0))
Donc si la tangente au graphe de f le coupe en
))
alors on a :
 = f(x_0+a) + (x-x_0-a)f'(x_0+a))
Soit

ou
 = 0)
Et si c'est bien cela, je ne vois pas vraiment comment le démontrer...
Merci d'avance pour votre aide !

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 20 Jan 2019, 18:02
par Sa Majesté » 20 Jan 2019, 18:02
Majaspique a écrit:Si j'ai bien compris :
L'équation de la tangente en

s'écrit :
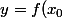 + (x-x_0)f'(x_0))
Donc si la tangente au graphe de f le coupe en
))
alors on a :
 = f(x_0+a) + (x-x_0-a)f'(x_0+a))
Salut,
Tu t'es mélangé les crayons.
Il faut remplacer

par
)
et

par

dans l'équation de la tangente en

.
Si la tangente au graphe de f le coupe en
))
alors on a :
 = f(x_0) + (x_0+a-x_0)f'(x_0))
 = f(x_0) + a f'(x_0))
Mais tout ça n'apporte rien puisque la pente de la tangente vaut
)
mais également
-f(x_0)}{a})
(pour

non nul) donc on a forcément
 = f(x_0) + a f'(x_0))
.
Le problème c'est de montrer que pour

donné, on peut trouver

tel que la tangente au graphe de f en

le coupe en
))
.
Prends un exemple concret : la fonction sinus et a=1 par exemple.
-
Majaspique
- Membre Naturel
- Messages: 96
- Enregistré le: 28 Nov 2017, 22:59
-
 par Majaspique » 20 Jan 2019, 18:35
par Majaspique » 20 Jan 2019, 18:35
Avec ton exemple ça donne ça :
https://prnt.sc/m9pqqnDonc l'idée serait de jouer sur la périodicité de la fonction pour montrer ça ? (ici pour a=
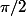
, la tangente en

coupe la courbe de f en (

) donc aussi en (
=1)
)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 20 Jan 2019, 18:50
par Ben314 » 20 Jan 2019, 18:50
Salut,
Vu que

est

-périodique, elle atteint son max. en un certain

et son min. en un certain

.
Si on pose
\!=\!af'(x)\!+\!f(x)\!-\!f(x\!+\!a))
, que peut tu dire de
)
? de
)
?
Qu'en déduit tu ?
(attention, il y a un piège là . . )Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
