Encadrement de Sn

[Nekster]

Bonjour,j'aurais besoin d'aide sur cette question svp

Soit Sn=Pi (somme des produits) de 1 a n de (1+(1/(K^3))
Prouvez que 3>Sn
Merci d'avance

(j'ai pas pu mettre les bornes ,mais c est de 1 a n)

[Ben314]

Salut,
La première méthode qui vient à l'esprit, c'est évidement une récurrence. Sauf que de montrer directement que par récurrence, ben c'est clair que ça risque pas de marcher vu que la suite est croissante donc on risque pas de démontrer une implication du type .
Donc pour démontrer un tel truc faut forcément mettre à droit du un truc variable (et majoré par 3 bien sûr). Donc personnellement, je regarderais à quelle condition (sur ) l'implication est vraie histoire de démontrer par récurrence que .

[Nekster]

j'ai essayé de trouver 'a' mais sans succes
tout ce que j'ai pu faire c'est ecrire Sn+1 =Sn* (1+(1/((n+1)^3))
mais je n'ai pas pu en deduire une condition sur alpha .

[Ben314]

On veut montrer par récurrence que .

Initialisation :
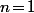
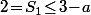
Pour on doit avoir donc on doit prendre .

Hérédité :
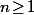
Supposons que pour un certain entier on ait .

Donc l'hérédité va fonctionner à condition d'avoir
Ce qui, après développement et mise au même dénominateur donne
Donc l'hérédité fonctionne à condition que pour tout

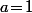
Bilan : Toute valeur vérifiant les deux condition en rouge va fonctionner. Pour faire au plus simple, on peut par exemple prendre vu que dans ce cas, on a pour absolument tout entier .

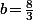
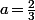
Et si ça t'amuse, si on fait la même chose avec , on montre facilement que la récurrence marche par exemple pour et ce qui donne un majorant un peu meilleur (à savoir ) de la suite .

[Nekster]

merci infiniment