Bonjour à tous !
Voici un exercice que je dois faire pour la rentrée ;
Calculer les équations des tangentes :
a) f(x) = (X+1)/(X-1) au point d'abscisse a=0
b) g(x) = racine carré de (x²-2x+2) au point d'abscisse a=1
c) h(x) = (x²+1)/(x²+x+1) au point d'abscisse a=0
A la question 1, j'ai commencé à faire ;
f(a+h) = [(0+h)+1] / [(0+h)-1] = (h+1)/(h-1)
f(a) = f(0) = -1
Ce qui me donne ;
[(h+1)/(h-1)] -(-1)
--------------------
h
En simplifiant, je trouve ;
2h
-----
h-1
Mais c'est là que je suis bloqué... J'ai déjà terminé ?
N'importe quel aide serait le bienvenue ! Merci
Fonctions et Dérivation
12 messages
- Page 1 sur 1
Re: Fonctions et Dérivation
a) C'est du gloubi-boulga à la sauce dérivée !
La tangente comme toutes les droites a une équation réduite de la forme
Tu as certainement vu en cours que l'équation réduite de la tangente au point) à la courbe d'équation
à la courbe d'équation 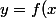) est
est 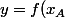 +f'(x_A) (x-x_A))
La tangente comme toutes les droites a une équation réduite de la forme
Tu as certainement vu en cours que l'équation réduite de la tangente au point
Re: Fonctions et Dérivation
ça nous donne ;
y= -1 + [(2h)/(h-1)] [h-(-1)]
y= -1 + (2h²+2h)/(h-1)
Mais ça nous donne pas vraiment un équation de la forme y=ax + b ?
y= -1 + [(2h)/(h-1)] [h-(-1)]
y= -1 + (2h²+2h)/(h-1)
Mais ça nous donne pas vraiment un équation de la forme y=ax + b ?
Re: Fonctions et Dérivation
Je ne comprends pas ce que vient faire ce h.
S'agit-il d'une tentative de retouver directement la valeur de la dérivée en 0 de la fonction=\frac{x+1}{x-1}) ?
?
Dans ce cas=\lim_{h\rightarrow0}\frac{f(0+h)-f(0)}{h})
Mais on ne te demande sûrement pas de repartir de la définition de la dérivée d'une fonction pour calculer f'(0)
f(x) est de la forme}{v(x)}) et l'expression de f'(x) figure dans tous les cours sur les dérivées
et l'expression de f'(x) figure dans tous les cours sur les dérivées
S'agit-il d'une tentative de retouver directement la valeur de la dérivée en 0 de la fonction
Dans ce cas
Mais on ne te demande sûrement pas de repartir de la définition de la dérivée d'une fonction pour calculer f'(0)
f(x) est de la forme
Re: Fonctions et Dérivation
Erreur de ma part, désolé ;
y= -1 + (2x²+2x)/(x-1)
J'ai donc trouvé l'équation de la tangente ?
y= -1 + (2x²+2x)/(x-1)
J'ai donc trouvé l'équation de la tangente ?
Re: Fonctions et Dérivation
Fais quand même l'effort de t'exprimer clairement.
Quest-ce qui est compliqué ?
- calculer la dérivée de=\frac{x+1}{x-1}) puis en déduire
puis en déduire ) ?
?
- chercher dans ton cours la formule de la dérivée de}{v(x)}) où
où  = x+1) et
et  = x-1) ?
?
Quest-ce qui est compliqué ?
- calculer la dérivée de
- chercher dans ton cours la formule de la dérivée de
Re: Fonctions et Dérivation
Ce qui me dérange le plus, c'est que j'ai du mal à savoir comment calculer f'(a)
Re: Fonctions et Dérivation
Tu n'as pas dû chercher beaucoup !
https://fr.wikipedia.org/wiki/Table_de_ ... s_usuelles
et
https://fr.wikipedia.org/wiki/Op%C3%A9r ... iv%C3%A9es
https://fr.wikipedia.org/wiki/Table_de_ ... s_usuelles
et
https://fr.wikipedia.org/wiki/Op%C3%A9r ... iv%C3%A9es
Re: Fonctions et Dérivation
J'ai réussi à mieux comprendre grâce à une vidéo, merci pour votre aide !
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

