Devoir maison

[Fleur974]

Bonjour je souhaiterais avoir de l'aide pour mon devoir de math s'il vous plaît !

Exercice :

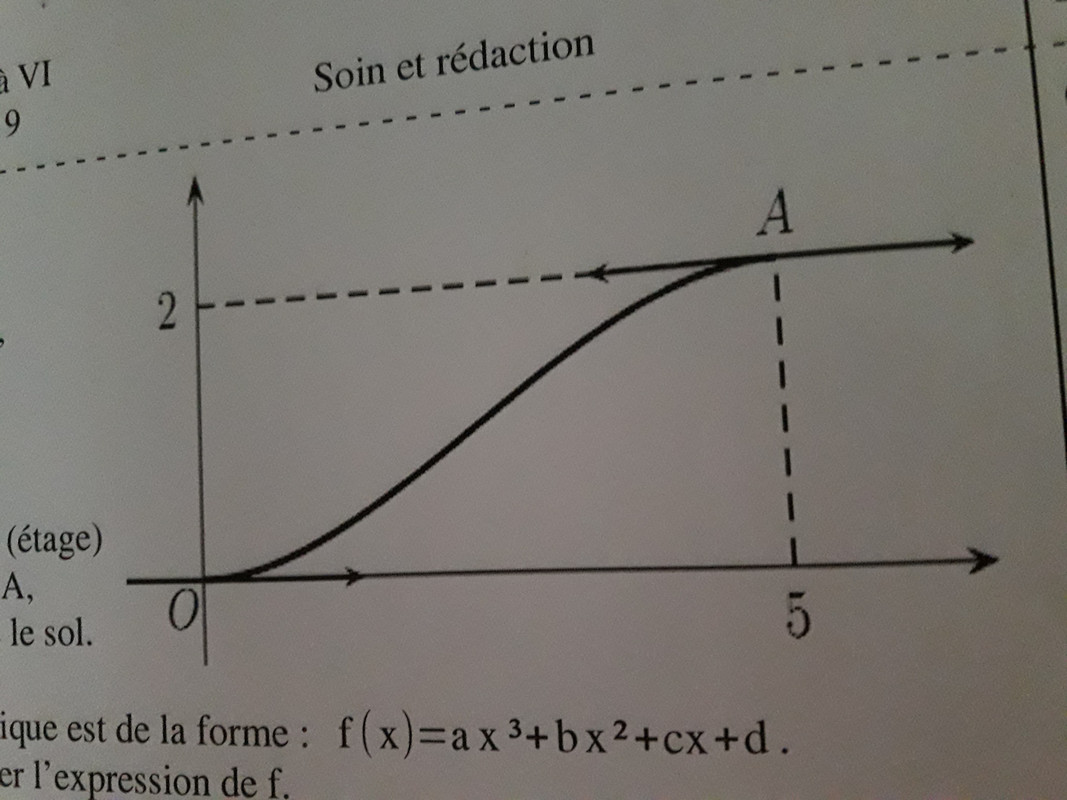
Pour permettre aux fauteuils roulants d'accéder à un étage situé 2 m plus haut, on construit une rampe ayant la forme représentée dans le repère ci-contre:( graphique joint au poste )

Il faut que la rampe:
- passe par O (rez-de-chaussée) et par A (étage)
- ait une tangente horizontale en O et en A, pour éviter de former des angles avec le sol

a) La fonction représentée sur ce graphique est de la forme: f(x)= ax^3 +bx² +cx +d
Calculer a, b, c et d afin ce déterminer l'expression de f.

b) Prouver que le point M, milieu de [OA], appartient à cette courbe.

c) Calculer la pente de la courbe en M. ( coefficient directeur de la tangente à(C) en M)

[Fleur974]

[img]file:///home/pop/Documents/graphique%202.png[/img]

[pascal16]

f(x)= ax^3 +bx² +cx +d
le dessin doit être mis sur un site en ligne pour qu'on la voit.

si f passe par O, on a f(0)=0
soit 0= a*0 + b*0 +c*0 +d
donc d= ...

il faut faire pareil pour les coordonnées et valeurs de la dérivée connues

[Fleur974]

Merci de m'avoir répondu .
Donc d=0

Pour la suite j'ai fait ceci :
f(5)=2 car C passe par le point A(5;2)
f'(0)=0 car C admet une tangente horizontale au point d'abscisse 0
f'(5) = ? car C admet au point A(5;2) une tangente de coefficient directeur ?

pour f'(5) je suis bloqué

[pascal16]

on a pas aussi une tangente horizontale ?

[Fleur974]

Si il y en a deux tangentes horizontales

[Fleur974]

[pascal16]

[pascal16]

f(x)= ax^3 +bx² +cx +d
f(0)=0
f(5)=2 car C passe par le point A(5;2)
f'(0)=0 car C admet une tangente horizontale au point d'abscisse 0
f'(5) = 0 car C admet au point A(5;2) une tangente horizontale

4 équations 4 inconnues

[Fleur974]

A partir de f(0) , on trouve d=0
A partir de f(5) , on trouve a=2
A partir de f'(5) , on trouve b=0
A partir de f'(0) , on trouve c=0

C'est bon ?

[pascal16]

f(x)= ax^3 +bx² +cx +d
f'(x)=3ax²+2bx+c

f(0)=0 implique d= 0
f'(0)=0 implique c = 0

f(5)=2 car C passe par le point A(5;2)
125a+25b=2

f'(5) = 0 car C admet au point A(5;2) une tangente horizontale
3*a*25+2*5*b=0

ton a et ton b ne me semblent pas bons

[Fleur974]

Je n'arrive pas à trouver a car le 2 m’embête

[pascal16]

(1) 125a+25b=2

(2) 3*a*25+2*5*b=0

"(1) *2-(2)*5" te donne a

[Fleur974]

=(125a+25b)*2-(3*a*25+2*5*b)*5
=250a+50b-375a-50b
=-125a
donc a=-125

[pascal16]

(1) 125a+25b=2
soit 250a+50b=4

(2) 3*a*25+2*5*b=0
soit 375a+50b=0

on soustrait : (375-250)a=-4

a=-4/125

[Fleur974]

J'ai tout compris sauf un point comment faites vous pour trouver -4 .

[pascal16]

exemple dans l'autre sens :
250a+50b=4
375a+50b=0

on soustrait les deux égalités membre à membre

250a+50b-(375a+50b)=4-0
...

[Fleur974]

Merci de m'avoir expliquer, je viens de comprendre !
Donc pour trouver b , nous remplacons a dans l'équation :
375a+50b=0
375*(-4/125)+50b =0
-12 +50 b =0
50b =12
b =12/50 =0,24

[Fleur974]

J'ai réussi à faire les autres questions j'aimerais savoir si c'est bon .

B) Prouvons que le point M est le milieu de [OA] et appartient à cette courbe :
O (0;0) A(5;2)
M= (x1+x2)/2
= (0+5)/2=5/2=2,5
M=(y1+y2)/2 = (0+2)/2=1

Donc M(2.5;1)
On en déduit que M est le milieu de [OA] , ainsi M appartient à cette courbe . En effet, les coordonnées du point M est la moitié des coordonnées du point A .

C) Pour calculer la pente , nous calculons le coefficient directeur :
M(2.5;1) A (5;2)

m= (delta y )/ (delta x )= (y A - y M )/(xA-xM )
= (2-1)/(5-2,5)
= 0.4

Faut - il faire autre chose ?

[pascal16]

les coordonnées du point M est la moitié des coordonnées du point A .
ARRGHGHGR, c'est sans doute comme ça qu'on le voit, mais la rédaction est à revoir, dis simplement que se sont les coordonnées du milieu de [OA]

C) Pour calculer la pente , nous calculons le coefficient directeur :
M(2.5;1) A (5;2)

m= (delta y )/ (delta x )= (y A - y M )/(xA-xM )
= (2-1)/(5-2,5)
= 0.4
Ca, c'est la pente moyenne entre O et A, on te dit de prendre la coefficient directeur de la tangente, c'est à dire le nombre dérivé en "M"