Problème Mathématique

[Zongo]

Bonjour à tous, j’ai un exercice à résoudre pour jeudi, mais je ne comprends pas par quel moyen passer afin de résoudre celui ci ou même comment le faire. L’énoncé est :

Sam Somme et Pierre Produit sont en classe lorsque leur enseignant donne à Sam la somme de 2 chiffres et Pierre le produit des 2 même chiffres (ces chiffres sont entre 2 et 9). Ils doivent trouver les chiffres.
Sam : je ne sais pas quels sont les chiffres, Pierre.
Pierre : Je savais que tu ne connaissais pas les chiffres... mais moi non plus.
Sam : Dans ce cas je connais les chiffres.
Quels sont les chiffres ?

[Ben314]

Salut,
A mon avis, le plus simple c'est de commencer par regarder ce que signifie le fait que Pierre, avec le produit des deux chiffres n'arrive pas en déduire la valeur des deux chiffre (et en supposant, ce que ne dit pas l'énoncé, que Pierre sait que les chiffres sont entre 2 et 9).
Et ce que ça signifie, c'est que le produit en question peut s'écrire d'au moins deux façons comme produit de deux chiffres entre 2 et 9. Par exemple, le produit pourrait être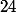 vu que mais aussi .
Quels sont tout les autres nombres qui peuvent s'écrire de plusieurs façon comme un produit (de deux entiers entre 2 et 9) ?
Indication : il y a 5 possibilités.

[Zongo]

Il y a 12 (2 x 6 et 3x 4)
16 : 2 x 8 et 4 x 4
18 : 2 x 9 et 3 x 6
24 : 3 x 8 et 4 x 6
36 : 4 x 9 et 6 x 6

[Ben314]

Oui, donc avec cette info là, on sait que les couples possibles, c'est :
( 2 ; 6 ) de somme 8
( 3 ; 4 ) de somme 7
( 2 ; 8 ) de somme 10
( 4 ; 4 ) de somme 8
( 2 ; 9 ) de somme 11
( 3 ; 6 ) de somme 9
( 3 ; 8 ) de somme 11
( 4 ; 6 ) de somme 10
( 4 ; 9 ) de somme 13
( 6 ; 6 ) de somme 12
Or, quand dans sa deuxième réponse Sam dit qu'il connaît les chiffres, ça signifie qu'en connaissant la somme et en sachant que la solution fait partie de celle çi dessus (vu qu'il a lui même fait le raisonnement qu'on vient de faire) il arrive à en déduire la valeur des deux chiffres. Ce qui signifie que cette somme n’apparaît qu'une seule fois dans la liste çi dessus.
Sauf que ça laisse quand même plusieurs possibilités :
- Soit la somme est 7 et les deux nombres sont 3 et 4.
- Soit la somme est 9 et les deux nombres sont 3 et 6.
- Soit la somme est 12 et les deux nombres sont 6 et 6.
- Soit la somme est 13 et les deux nombres sont 4 et 9.
Et ces 4 solutions sont toutes les 4 parfaitement cohérentes avec l'énoncé.