SUITE TERMINALE S

[rabiia]

Bonjour j’ai besoin d’aide pour l’exo 2 de mon DM merci d´avance

[jlb]

salut utilise la question 1)

1 +1/4 +1/9....<1 + 1/(2*1) + 1/(3*2)…..=1 + (1/1-1/2) + (1/2 - 1/3) et plein de termes se simplifient.


sinon, il y a un erreur dans l'énoncé, la somme part de k=1 et pas de k=0

[rabiia]

Enfaite je n’ai pas fais la première question je comptais faire un raisonnement par réc mais je bloque a l´hérédité

[jlb]

bah, transforme 1/(k-1) - 1/k pour voir ce que cela donne et ensuite essaie de comprendre pourquoi c'est forcément plus grand que 1/k²

[titine]

En réduisant au même dénominateur : 1/(k-1) - 1/k = (k-k+1)/(k(k-1)
= 1/(k(k-1))
Or, pour tout k >= 2 : k-1 < k
Donc k(k-1) < k^2
Donc 1/(k(k-1)) > 1/k^2

[fastandmaths]

Bonsoir,

Je n' ai rien compris à la question moi aussi, il y a une erreur dans l'énoncé car la borne est fausse. La somme existe à partir de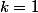 et en plus celle ci n 'est jamais ,d’où mon incompréhension .
on a



donc

donc

La somme est inférieur à 2 non?

D'ailleurs, pour faire autrement



donc




la somme serait supérieur et ne dépasserait pas .L'énoncé dit le contraire , pouvez vous m'expliquez ou est l'erreur ?

Merci,

[LB2]

Bonsoir,

il y a une erreur d'énoncé : il faut lire k=2 à n dans la question 2.
On aurait d'ailleurs pu définir la suite (un) à cette question plutôt qu'à la question 3.

[LB2]

Pour la culture, la somme des inverses des carrés 1+1/4+1/9+1/16+... , qui est donc convergente d'après l'exercice, vaut 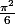. Ce résultat a été démontré par Euler à l'aide de plusieurs méthodes, rendues parfaitement rigoureuses par ses successeurs.
On définit plus généralement la fonction zéta de Riemann comme la fonction qui à la variable associe la somme +...

[fastandmaths]

Bonsoir

la somme converge vers , c 'est puissant de retrouver caché dedans. Merci LB2