Exercice second degré 1ère ES/L

[Tortue]

Bonjour, j'ai un DM pour la rentrée et je ne parviens pas à le résoudre. Je me permets de vous demander de l'aide. J'ai résolu les trois quarts de l'exercice mais je ne parviens pas à répondre aux deux dernières questions.

Enoncé :

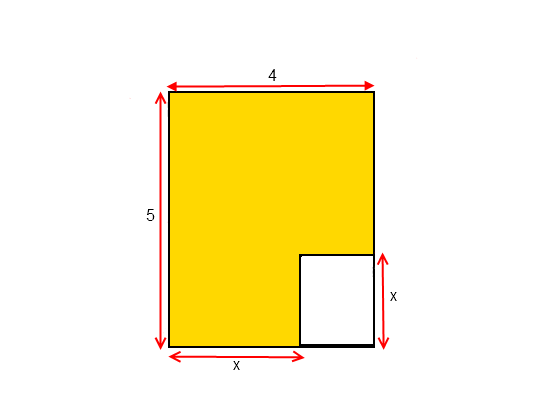
L'entreprise Prim'Jet se propose de réaliser un logo représentant la lettre P stylisée, dans une pièce métallique rectangulaire d'épaisseur 5 mm. Sur la figure suivante, la partie colorée représente la zone où le matériau doit être déposé. Les cotes sont exprimés en cm et 0 supérieur ou égal à x inférieur ou égal à 4.
On note A l'aire de la partie traitée (colorée sur le schéma).



1. Calculer A pour x= 1,5.

J'ai donc fait 4 - 1,5 = 2,5 cm
Puis j'ai cherché à calculer l'aire rectangle total et lui ai soustrait l'aire du petit rectangle blanc (afin d'obtenir l'aire du P).
(4 * 5) - (2,5 * 1,5) = 20 - 3,75 = 16,25
A = 16,25 cm²

2. a) Exprimer l'aire du rectangle découpé (blanc sur le schéma) en fonction de x.

Ici j'ai fait x (4 - x) ce qui me donne 4x - x².

b) En déduire que l'aire A est donnée par la relation : A = x² - 4x + 20

Ici je ne comprends pas vraiment car pour moi l'aire de A équivaut à :
A = (4*5) - [(4 - x) *x] soit 20 - 4x - x²

Il doit sans doutes y avoir une erreur dans mon raisonnement mais je ne comprends pas laquelle...

3. L'entreprise qui a commandé les pièces propose une aire de 17 cm². Déterminer par le calcul (la ou les) cote(s) x correspondante(s).

Je me suis donc dit que j'allais utiliser delta afin de calculer les deux x. Mais je n'ai pas réussi.
Voici ce que j'ai fait :

x² - 4x + 20 = 17

a = 1
b = (-4)
c = 20

Donc delta = b² - 4ac
= 4²- 4 * 1 * 20
= 16 - 4*20
= 16 - 80
= (-64)

Or la racine d'un nombre négatif est impossible... Il n'y aurait donc pas de solution ? Ici aussi mon raisonnement est sans doutes faux mais je n'arrive pas à comprendre pourquoi.

Je vous remercie d'avance pour votre aide.
Passez une bonne journée !

[Ben314]

Salut,

b) En déduire que l'aire A est donnée par la relation : A = x² - 4x + 20
Ici je ne comprends pas vraiment car pour moi l'aire de A équivaut à :
A = (4*5) - [(4 - x) *x] soit 20 - 4x - x²

On va revenir à du basique de chez basique :
Mettons que tu ait A=20 Euros en poche et que tu achète deux trucs, l'un à B=3 Euros puis un autre à C=5 Euros.
- Est-tu d’accord avec le fait que tes achat s'élèvent à B+C=8 Euros ?
- Est-tu d’accord avec le fait que ce qu'il te reste, c'est A-(B+C) = 20 - 8 = 12 Euros ?
- Si on part différemment, est tu d'accord avec le fait qu'après l'achat de B, il te reste A-B = 20 - 3 = 17 Euros ?
- Puis qu'ensuite, après l'achat de C, il te reste (A-B) - C = 17 - 5 = 12 Euros ?

Bref, A-(B+C) c'est égal à A-B-C et pas à A-B+C : si tu achète deux trucs, soit tu fait la somme des achat puis tu retranche cette somme à ton capital de départ, soit tu retranche l'un puis tu retranche l'autre des deux achats de ton capital de départ.

[Tortue]

Salut,

b) En déduire que l'aire A est donnée par la relation : A = x² - 4x + 20
Ici je ne comprends pas vraiment car pour moi l'aire de A équivaut à :
A = (4*5) - [(4 - x) *x] soit 20 - 4x - x²

On va revenir à du basique de chez basique :
Mettons que tu ait A=20 Euros en poche et que tu achète deux trucs, l'un à B=3 Euros puis un autre à C=5 Euros.
- Est-tu d’accord avec le fait que tes achat s'élèvent à B+C=8 Euros ?
- Est-tu d’accord avec le fait que ce qu'il te reste, c'est A-(B+C) = 20 - 8 = 12 Euros ?
- Si on part différemment, est tu d'accord avec le fait qu'après l'achat de B, il te reste A-B = 20 - 3 = 17 Euros ?
- Puis qu'ensuite, après l'achat de C, il te reste (A-B) - C = 17 - 5 = 12 Euros ?

Bref, A-(B+C) c'est égal à A-B-C et pas à A-B+C : si tu achète deux trucs, soit tu fait la somme des achat puis tu retranche cette somme à ton capital de départ, soit tu retranche l'un puis tu retranche l'autre des deux achats de ton capital de départ.

Oui, je suis d'accord mais si l'aire totale de mon grand rectangle correspond à A et que l'aire du petit rectangle blanc correspond à B et celle de la forme jaune à C. Je sais que A = B + C
Alors pourquoi lorsque je fais A - B je n'obtiens pas C ? Pourquoi est ce que si je fais l'aire du grand rectangle moins celle du petit blanc je n'obtiens pas l'aire de la forme jaune ?
De plus il n'y a pas de reste ici....

Et lorsque je résous l'équation 20 = 4x + x² = (4-x)x j'obtiens bien 0....

[Ben314]

A = (4*5) - [(4 - x) *x] = 20 - [ 4x - x^2 ] = 20 - [ 4x + (-x^2) ] = 20 - 4x - (-x^2) = 20 - 4x + x^2

[Tortue]

3. L'entreprise qui a commandé les pièces propose une aire de 17 cm². Déterminer par le calcul (la ou les) cote(s) x correspondante(s).

Je me suis donc dit que j'allais utiliser delta afin de calculer les deux x. Mais je n'ai pas réussi.
Voici ce que j'ai fait :

x² - 4x + 20 = 17

a = 1
b = (-4)
c = 20

Donc delta = b² - 4ac
= 4²- 4 * 1 * 20
= 16 - 4*20
= 16 - 80
= (-64)

Or la racine d'un nombre négatif est impossible... Il n'y aurait donc pas de solution ? Ici aussi mon raisonnement est sans doutes faux mais je n'arrive pas à comprendre pourquoi.

Mis à part cela je crois avoir compris mon erreur pour la dernière question. J'ai laissé le = 17 alors qu'il fallait le soustraire à l'équation. Cela donne donc : x² - 4x + 3 = 0 (au lieu de x² - 4x + 20 = 17)
Je vais essayer le tout recalculer.

[Tortue]

A = (4*5) - [(4 - x) *x] = 20 - [ 4x - x^2 ] = 20 - [ 4x + (-x^2) ] = 20 - 4x - (-x^2) = 20 - 4x + x^2

D'accord ! Je crois avoir compris mon erreur ! En fait le 4x correspond à tout le bas du rectangle. Il faut donc soustraire le carré blanc à celui ci (soit soustraire x²) . Je ne suis pas sûre que ce que je suis en train de dire soit très claire mais en tous cas je crois avoir compris ce qui n'allait pas ! Merci beaucoup !

[Ben314]

Je me suis donc dit que j'allais utiliser delta afin de calculer les deux x. Mais je n'ai pas réussi.
Voici ce que j'ai fait :
x² - 4x + 20 = 17
a = 1
b = (-4)
c = 20
Donc delta = b² - 4ac
= 4²- 4 * 1 * 20
= 16 - 4*20
= 16 - 80
= (-64)
Or la racine d'un nombre négatif est impossible... Il n'y aurait donc pas de solution ? Ici aussi mon raisonnement est sans doutes faux mais je n'arrive pas à comprendre pourquoi.

Ben évidement que c'est faux : les science, ça fait un bon moment que c'est plus de l'alchimie où on applique "des recettes magiques" sans rien y comprendre.

Le résultat de cours que tu as où il est question de ce fameux discriminant = b² - 4ac, c'est ça :
Si on doit résoudre une équation de la forme où sont des réels ne dépendant pas de et où alors blablabla.
Et, bien évidement, comme tout les résultat, c'est pas du "gratuit", c'est à dire que pour pouvoir appliquer le bidule, il y a des conditions à vérifier.
Ici,
- Est ce que l'équation (en rouge dans ton post) est bien de la forme mentionnée par le théorème ?
- Est ce que a,b,c sont bien des réels ne dépendant pas de x ?
- Est ce que ?

[Tortue]

Je me suis donc dit que j'allais utiliser delta afin de calculer les deux x. Mais je n'ai pas réussi.
Voici ce que j'ai fait :
x² - 4x + 20 = 17
a = 1
b = (-4)
c = 20
Donc delta = b² - 4ac
= 4²- 4 * 1 * 20
= 16 - 4*20
= 16 - 80
= (-64)
Or la racine d'un nombre négatif est impossible... Il n'y aurait donc pas de solution ? Ici aussi mon raisonnement est sans doutes faux mais je n'arrive pas à comprendre pourquoi.

Ben évidement que c'est faux : les science, ça fait un bon moment que c'est plus de l'alchimie où on applique "des recettes magiques" sans rien y comprendre.

Le résultat de cours que tu as où il est question de ce fameux discriminant = b² - 4ac, c'est ça :
Si on doit résoudre une équation de la forme où sont des réels ne dépendant pas de et où alors blablabla.
Et, bien évidement, comme tout les résultat, c'est pas du "gratuit", c'est à dire que pour pouvoir appliquer le bidule, il y a des conditions à vérifier.
Ici,
- Est ce que l'équation (en rouge dans ton post) est bien de la forme mentionnée par le théorème ?
- Est ce que a,b,c sont bien des réels ne dépendant pas de x ?
- Est ce que ?

Oui oui je sais je l'ai dit plus haut (je me suis déjà corrigée dans un autre message), j'ai fait une erreur stupide puisque mon équation n'était pas égale à 0

Ducoup j'ai tout recalculé et j'ai trouvé comme solutions S = [ 0 ; 3 ]

[Ben314]

Ducoup j'ai tout recalculé et j'ai trouvé comme solutions S = [ 0 ; 3 ]

J'ai de gros doutes concernant le fait que, lorsque x=0, le nombre x² - 4x + 20 soit égal à 17.

P.S. Et, en math., la notation [0;3] avec des crochets, ça désigne l'intervalle d'extrémité 0 et 3, c'est à dire l'ensemble de tout les réels entre 0 et 3 (inclus). Et ça m'étonnerais que ton équation ait autant de solutions que ça. L'ensemble contenant uniquement les réels 0 et 3 (et rien d'autre), ça se note {0;3} avec des accolade et pas des crochets.