Somme d'une indicatrice

[Menthix]

Bonjour,
Je ne comprends pas pourquoi la série entière : Somme(Indicatrice(N>k)) = N.
Avec N une variable aléatoire discrète définie sur l'ensemble des entiers naturels et k un entier naturel.
Pourriez-vous m'expliquer ? Merci d'avance

[Ben314]

Salut,


P.S. Et visiblement tu as rien compris à ton truc : "ton" k, c'est pas "un entier naturel", c'est l'indice sur lequel on fait la somme et cet indice k décrit l'ensemble des entiers naturels et il est totalement absent de la relation de départ (c'est une "variable muette")

[Menthix]

Salut,
Merci de ta réponse
Non désolé j'ai jamais entendu parler de cette identité remarquable / Elle a un nom pour que je regarde sur google ? Je voudrais voir la démo. Merci d'avance

[Menthix]

Sinon je comprends toujours pas désolé...

[LB2]

Soit .

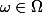
La variable aléatoire indicatrice vaut 1 si , et 0 sinon.
A omega fixé, la somme des indicatrices est donc finie et vaut .

[Lostounet]

Salut,
Merci de ta réponse
Non désolé j'ai jamais entendu parler de cette identité remarquable / Elle a un nom pour que je regarde sur google ? Je voudrais voir la démo. Merci d'avance

Quand même...
Prends un entier N par exemple N=5
Pour tout entier k, Indicatrice(N>k) est égale à 1 si N>k et 0 si N<=k. (Ça c'est la définition d'une indicatrice...).

Donc:
Somme(Indicatrice(5>k))
= Indicatrice(5>0) + Indicatrice (5>1)
+....Indicatrice(5>4) + Indicatrice(5>5) + Indicatrice(5>6)+....

= 1 + 1 + 1 + 1 + 1 + 0 + 0......
= 5

[pascal16]

J'y connais rien en VA mélangées à des indicatrices (et Ben va s'énerver de questions trop bêtes pour être posées).

Somme(Indicatrice(N>k)) = N

on a en gros f(n) -> n fois (une chose vraie=1) -> n
Ca, c'est ce que je comprends pour une fonction indicatrice, mais on a des VA


on a ici " Avec N une variable aléatoire discrète "
Si N est une VA, on doit démonter une égalité de VA (et chaque élément de la somme est une VA ?)
en particulier N peut valoir 0 presque partout et 1/p pour p valeurs.
Comment remonter à une VA ?

[LB2]

Ce qui est sur c'est que en sommant n fois 1, ben, on trouve n. C'est ce que tu dis pascal.


Les v.a. sont égales ssi elles coincident sur l'univers grand Omega (cf mon post ou je montre l'égalité des v.a. pour toute issue élémentaire petit omega).
Pas besoin de connaître la loi de N pour que cette égalité soit vraie.