Une question sur la fonction indicatrice

[Als128]

Ca me parait évident mais bon...
Comme je maitrise pas toutes les propriétés de la fonction, une aide est la bienvenue.
Est ce que
?

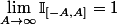
Merci

[gigamesh]

Bonjour,
attention, c'est une "suite" (pas vraiment vu qu'on a pas forcément A entier) de fonctions dont tu cherches la limite !

En tout cas pour A>|x| on a donc on peut dire que la fonction indicatrice de l'intervalle [-A;A] converge simplement vers la fonction constante 1 ; mais bien sûr il ne s'agit pas d'une convergence uniforme !

[Als128]

Donc ca veut bien dire que
tend vers quand tend vers l'infini ?

[gigamesh]

Pour x fixé, oui.

[Als128]

oki donc si u est définie partout, l'égalité est vraie pour tout x. C'est ca ?

[Doraki]

Ben on a que pour tout x dans R et pour tout A >= 0,
uA(x) = 0 si A < |x|
uA(x) = u(x) si A >= |x|.

A partir de là, c'est rapide de conclure que pour tout x, la limite quand A tend vers l'infini de uA(x) vaut bien u(x).

[Dihtbscii]

Oui. Et si u(x) tend vers 0 quand |x| tend vers +00, tu as même la convergence uniforme