Coniques

[Khotidom]

Bonsoir,

Jai un exercice sur les coniques a rendre. Est-ce que vous pourriez m'aider ?

Le voici : Soit À et B 2 points distincts du plan, I le milieu de [AC]
1) Déterminé l'ensemble des points M du plan tels que :MI^2 =MA X MB
2) Determlne la nature de ce lieu ainsi que tout ses paramètres
3) Quelle particularité présente ce lieu géométrique ?

[mehdi-128]

Il faut passer par les coordonnées des points.

On note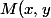

Vous avez quelles coordonnées pour et ?

[Khotidom]

Je n'ai aucune coordonnée pour les points À et B... voilà pourquoi je suis perdu..

[Pisigma]

Bonjour,

tu peux toujours choisir un système d'axes tel que A=(0;0); B=(b;0)

d'où les coordonnées de I milieu de [AB], je suppose

[mehdi-128]

Bonjour,

tu peux toujours choisir un système d'axes tel que A=(0;0); B=(b;0)

d'où les coordonnées de I milieu de [AB], je suppose

Bien vu je me disais faut introduire un repère.

Du coup il devrait d'abord calculer les coordonnées du point I puis : , et enfin puis en déduire leur norme.

[aviateur]

Bonjour
C'est tout à fait possible de vouloir passer par un système de coordonnées. Dans ce cas il faut respecter le rôle symétrique jouer par A et B. Donc prendre par exemple A=(-1,0) et B(0,1).

[mehdi-128]

Bonjour
C'est tout à fait possible de vouloir passer par un système de coordonnées. Dans ce cas il faut respecter le rôle symétrique jouer par A et B. Donc prendre par exemple A=(-1,0) et B(0,1).

On trouvera la même chose si on prend d'autres points pour A et B ?

[aymanemaysae]

Bonjour;

En adoptant la méthode d' "Aviateur" , tu auras : A(1 ; 0) , B(- 1 ; 0) et I(0 ; 0) , donc I est l'origine

du repère orthonormé que tu as choisi .

Soit M(x ; y) un point du plan qui vérifie la condition donnée ; donc :

IM² = x² + y² ; MA² = (x - 1)² + y² et MB² = (x + 1)² + y² ;

donc on a : MI^4 = MA² . MB² .

A toi de continuer et conclure .

[aviateur]

On trouvera la même chose si on prend d'autres points pour A et B ?

A et B sont distincts. C'est tout. Il n'y a qu'une seule configuration. Comment pourrait-on trouver autre chose?

La réponse c'est que l'on aura une hyperbole équilatère dont il faudra déterminer les foyers et la directrice par rapport aux points A et B.
Personnellement je pense que choisir un système de coordonnées est une bonne idée. Mais choisir un système de coordonnées qui alourdit les calculs, je vois pas l'intérêt et là c'est pas une bonne idée.

[Pisigma]

Aviateur :j'ai trouvé une hyperbole aussi mais c'est plus compliqué comme calcul.Tes coordonnées conduisent à des calculs plus simples.

[aviateur]

Oui, si tu regardes bien lorsqu'on étudie une conique on essaye toujours de l'écrire dans un repère où l'équation est la plus simple possible (équation réduite).
A la limite tu prends n'importe quoi, A=(3,7) B=(-5,3) par exemple tu va trouver que c'est une conique mais pas si vite que c'est une hyperbole.
Maintenant il ne faut pas oublier que l'on demande les foyers, la directrice, l' excentricité. Bon les foyers on les devine. Mais la directrice, l'excentricité. Il y des calculs à faire. Autant qu'ils soient les +simples possibles.

J'ai une remarque à faire concernant le passage à un repère. Ce n'est pas obligatoire. En effet
l'équation peut surement se mettre sous la forme |MA-MB|=2a
Alors ayant trouvé a on peut remonter à toutes les caractéristiques de l'hyperbole.

[aviateur]

cqfd