Les coniques : Problèmes de tangente
20 messages
- Page 1 sur 1
Les coniques : Problèmes de tangente
Sujet du devoir
Bonjour,
Calcule une équation cartésienne de la tangente à l'ellipse E = 3x² + 5y² - 15 = 0 en ses points dont l'abscisse égale l'ordonnée.
Où j'en suis dans mon devoir
Je ne sais pas du tout comment m'y prendre pour commencer cet exercice. J'ai vu en cours comment trouver l'équation d'une tangente à f à un certain point (avec la dérivée) mais ici on parle d'abscisse égale à l'ordonnée donc je suis perdu. Quelqu'un sait m'aider ?
Merci
Bonjour,
Calcule une équation cartésienne de la tangente à l'ellipse E = 3x² + 5y² - 15 = 0 en ses points dont l'abscisse égale l'ordonnée.
Où j'en suis dans mon devoir
Je ne sais pas du tout comment m'y prendre pour commencer cet exercice. J'ai vu en cours comment trouver l'équation d'une tangente à f à un certain point (avec la dérivée) mais ici on parle d'abscisse égale à l'ordonnée donc je suis perdu. Quelqu'un sait m'aider ?
Merci
via l'analyse
bonjour,
i) par l'algèbre
pose y=mx+p
on remplace dans l'équation de (E)
et ensuite tu dis ensuite que le trinome du second degré en a une racine double.
a une racine double.
zut, j'ai répondu avant d'avoir fait les calculs :hum:
ii) par l'analyse
(x-x_0)+<br />\frac{\partial \, f}{\partial \, y}(x_0,y_0) (y-y_0)=0)
avec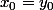
i) par l'algèbre
pose y=mx+p
on remplace dans l'équation de (E)
et ensuite tu dis ensuite que le trinome du second degré en
zut, j'ai répondu avant d'avoir fait les calculs :hum:
ii) par l'analyse
avec
mathelot a écrit:bonjour,
i) par l'algèbre
pose y=mx+p
on remplace dans l'équation de (E)
et ensuite tu dis ensuite que le trinome du second degré ena une racine double.
zut, j'ai répondu avant d'avoir fait les calculs :hum:
ii) par l'analyse
avec
Je préfère résoudre cette exercice par l'algèbre. Quand on a remplacé y dans l'équation, je dois utiliser ro (b²-4ac) ?
Est-ce que je peux isoler y dans l'équation de l'ellipse et puis dire que x=y ?
Merci
mathelot a écrit:est la dérivée, relativement à
,
du polynomeen x et y :
et
est ce au programme, ce qu'on appelle les dérivées partielles ?
Le problème c'est que je ne vois pas du tout ce qu'est x0 et y0. Voici ce que j'ai fait : j'ai isolé y et puis comme x=y, j'ai x = V(3-3x²/5) et x = -V(3-3x²/5) mais là je ne sais pas comment continuer
x,y coordonnées génériques d'un point du plan.
Avec ces coordonnées, on teste l'appartenance du
point M(x;y) à l'ellipse.
l'indice dans signifie que l'abscisse est fixée (=constante)
signifie que l'abscisse est fixée (=constante)
) est un point fixé (=non variable, choisi) de l'ellipse.
est un point fixé (=non variable, choisi) de l'ellipse.
avec tes calculs, remplace x par et élève au carré.
et élève au carré.
Comme ça, on calcule
réponse ci-dessous:
x_0=+- V(15)/(2V2)
Avec ces coordonnées, on teste l'appartenance du
point M(x;y) à l'ellipse.
l'indice dans
avec tes calculs, remplace x par
Comme ça, on calcule
réponse ci-dessous:
x_0=+- V(15)/(2V2)
mathelot a écrit:que dit le cours ? est ce que les dérivées partielles sont au programme ?
Je suis belge et je pense que les méthodes ne sont pas les mêmes. Je connais les dérivées mais pas les partielles. Donc, j'ai 2 points de tangence qui sont (V30/4 ; V30/4) et (-V30/4 ; -V30/4). Si je dois dériver, ça va faire 0 vu que c'est une constante...
Salut
A la rigueur, si on ne veut pas utiliser les dérivées partielles, on peut utiliser l'affinité qui transforme le cercle de diamètre [AB] en l'ellipse de grand axe [AB].
On peut ainsi trouver les coordonnées de C, intersection de l'axe des x et de la tangente cherchée.
On trouve pour l'abscisse de C en utilisant l'égalité:
pour l'abscisse de C en utilisant l'égalité: 
Ensuite, il faut écrire une équation de droite connaissant les coordonnées de deux points.

A la rigueur, si on ne veut pas utiliser les dérivées partielles, on peut utiliser l'affinité qui transforme le cercle de diamètre [AB] en l'ellipse de grand axe [AB].
On peut ainsi trouver les coordonnées de C, intersection de l'axe des x et de la tangente cherchée.
On trouve
Ensuite, il faut écrire une équation de droite connaissant les coordonnées de deux points.

solution algébrique
soit) les coordonnées d'un point de tangence (il y en a deux)
les coordonnées d'un point de tangence (il y en a deux)
soit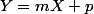 une équation de la tangente
une équation de la tangente
) vérifie les deux équation, ce qui donne:
vérifie les deux équation, ce qui donne:
^2-15=0) .
.
+10 mpx_0 +p^2-15=0) .
.
c'est une équation du second degré en avec racine double , on lui annule son
avec racine double , on lui annule son 
(l'abscisse d'un point de tangente est racine double de son équation)
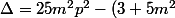(p^2 - 15)=0)
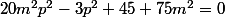
+4+75m^2&=&0 \\<br />p&=&x_0(1-m)<br />\end{array}<br />\right.)
 ayant été calculé, ça fait deux relations pour calculer
ayant été calculé, ça fait deux relations pour calculer 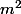 puis
puis 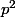
soit
soit
c'est une équation du second degré en
(l'abscisse d'un point de tangente est racine double de son équation)
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
