Suites Ts

[Mama27]

Bonjour, j aurais encore besoin d aide svp je ne vois pas ce que l énoncé veut dire par conclure a la derniere question le voici :

On considère la suite (Un) definie par :
Uo=1 et, pour tout entier naturel n,
Un+1=((n+1)/(2n+4)Un
On définit la suite Un par : pour tt entier naturel n, Vn=(n+1)Un.
L objectif de l exo est de determiner l expression de Un en fonction de n . Pour cela on s aidera d une feuille de calcul pour emettre une conjecture que l on validera par une démonstration.

1. Creer une feuille de calcul, sur un tableur, qui presente les valeurs des 1ers termes des suites Un et Vn, arrondies au cent millieme pres.
Recopier la formule sur la copie saisie dans la cellule B3 de la feuille de calcul et qui étirée ensuite vers le bas, permet d obtenir les termes succesifs de Un ?

Pour cette question j ai reussi a faire le tableur ainsi que la formule ((A2+1)/(2*A2+4)*B2

2. Conclure
C est ici que je n ai pas compris j ai ecrit la suite semblr tendre vers moins l infini
Mais je n arrive pas a definir n en fonction de Un +1
Je ne sais mm pas si c est cela qu il faut faire
Un peu d aide svp...

[hdci]

Bonjour,

2. Conclure
C est ici que je n ai pas compris j ai ecrit la suite semblr tendre vers moins l infini
Mais je n arrive pas a definir n en fonction de Un +1
Je ne sais mm pas si c est cela qu il faut faire

Comment peux-tu trouver une limite ? tous les termes sont positifs, quand on multiplie des nombres positifs entre eux on obtient des nombres positifs .

Autre question : quand tu écris Un+1=((n+1)/(2n+4)Un (il manque une parenthèse), veux-tu dire que c'est
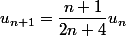? Auquel cas sous Excel on "voit" que la limite (des deux suites) est nulle.

[Mama27]

Ah oui pardon la suite tend vers 0 non ?
Et oui pour la suite c est ca que j ai voulu dire

[hdci]

Oui la suite (les deux suites d'ailleurs) tend(ent) vers 0.

Si par "conclure" il suffit d'exploiter ce que permet de conjecturer Excel c'est terminé.

Sinon il faut montrer que la limite est bien nulle.

En manipulant la fraction , peux-tu montrer que ce nombre est inférieur à ?

Du coup, peux-tu borner la suite par une suite géométrique dont la limite est connue ?

[Mama27]

Heu par contre je ne suis pas sure d arriver a demontrer que la limite est nulle par calcul
Et le terme borner une suite je n ai jamais vu pouvez vous m expliquer svp ?
Mais il ne faut pas determiner Un en fonction de n pour la question 2 ? J ai demandé a mon prof mais il ne m a pas vraiment repondu

[pascal16]

Vn=(n+1)Un.

que vaut V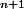 en fonction de

remplace Un+1 en fonction de Un

il y a un simplification

on retrouve une relation simple entre Vn+1 et Vn ... qui ressemble à la méthode de hdci

[Mama27]

Je trouve ceci
Vn+1=(n+1+1)Un+1
=(n+2)Un+1
=(n+2)((n+1)/(2n+4)Un
=((n+2)×(n+1))/(2n+4)
=((n^2+3n+2)/2n+4)Un

[hdci]

Je trouve ceci
Vn+1=(n+1+1)Un+1
=(n+2)Un+1
=(n+2)((n+1)/(2n+4)Un
=((n+2)×(n+1))/(2n+4)
=((n^2+3n+2)/2n+4)Un

L'erreur de débutant, à ne pas commettre, c'est de développer. Il faut factoriser au maximum (c'est vrai en général pour n'importe quel problème). C'est uniquement quand la factorisation ne donne rien de plus que tu peux penser à développer pour voir si quelque chose va se simplifier.
Au numérateur, tu as donc
Au dénominateur, du as . Comment peux-tu factoriser cela ?
Après quoi tu trouves une simplification évidente. Il n'y a plus qu'à utliser la définition de .