Bonjour, j aurais besoin d un peu d aide svp
On considere la suite (Un) definie par U0=U1=1 et, pour tt entier n superieur ou egal a 2 :
Un =Un-1+Un-2
On pose ø=(1+V5)/2
1. Verifier que ø^2=ø+1
Cette question j y suis arrivée. Mais c est apres que ca bloque j arrive a développé mais je n arrive pas a obtenir la forme a+øb
2. En déduire une expression de ø^3, ø^4, ø^5 de la forme a+øb, avec a et b deux entiers.
3.4.5. Je n ai pas encore regardé.
Suites Ts
10 messages
- Page 1 sur 1
Re: Suites Ts
Salut,
En fait l'astuce est de dire que comme ø^2=ø+1
Alors en multipliant les deux côtés par ø:
ø^3=ø( ø+1 ) = ø^2 + ø
Mais n'oublie pas que ø^2=ø+1
Ce qui veut dire que ø^3= ø^2 + ø = ø+1 + ø = 2ø+1
Bien sûr tu peux ne pas utiliser cette astuce et mener des calculs (assez longs) en développant explicitement.
En fait l'astuce est de dire que comme ø^2=ø+1
Alors en multipliant les deux côtés par ø:
ø^3=ø( ø+1 ) = ø^2 + ø
Mais n'oublie pas que ø^2=ø+1
Ce qui veut dire que ø^3= ø^2 + ø = ø+1 + ø = 2ø+1
Bien sûr tu peux ne pas utiliser cette astuce et mener des calculs (assez longs) en développant explicitement.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Suites Ts
Salut,
Tu peut effectivement tout développer, mais l'énoncé avec son "en déduire que..." est là pour t'inciter plus que fortement à utiliser la question précédente comme le fait Lostounet (c'est souvent très utile de bien lire l'énoncé)Lostounet a écrit:Bien sûr tu peux ne pas utiliser cette astuce et mener des calculs (assez longs) en développant explicitement.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suites Ts
Ben314 a écrit:(c'est souvent très utile de bien lire l'énoncé)
Le pire c'est que je ne lis plus les énoncés avant de répondre ... tu t'adresses à moi on dirait ! Mdr
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Suites Ts
Ou bien... à moi... vu que les énoncé de "Lycée", je les lit toujours en diagonale et je me rend souvent compte ensuite que l'idée que je suggère n'est pas celle attendue (y'a aussi des fois où je trouve que celle "attendue" est complètement con, mais là, c'est une autre histoire).Lostounet a écrit:Le pire c'est que je ne lis plus les énoncés avant de répondre ... tu t'adresses à moi on dirait ! Mdr
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suites Ts
Merci bcp a vous de m avoir repondu cela m a vraiment aidé j etais partie dans des calculs impossibles je me suis retrouvée avec des fractions je pars toujours bcp trop loin
Donc j ai trouvé:
ø^3=2ø+1
ø^4=3ø+1
ø^5=4ø+1
Est ce correct ?
Donc j ai trouvé:
ø^3=2ø+1
ø^4=3ø+1
ø^5=4ø+1
Est ce correct ?
Re: Suites Ts
Pour ø^3=2ø+1, c'est bon.
Par contre ø^4 = ø ø^3 = ø
ø^3 = ø (2ø+1) = 2ø^2+ø = 2(ø+1)+ø = 3ø+2
(2ø+1) = 2ø^2+ø = 2(ø+1)+ø = 3ø+2
Par contre ø^4 = ø
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suites Ts
Ah oui d accord j avais oublié un passage dans mon calcul
Donc ø^5= ø×ø^4
=ø(3ø+2)=3ø^2+2ø
=3×(ø+1)+2ø
=3ø+3+2ø
=5ø+3
???
Mais avant je voyais la récurrence a faire dans la prochaine question mais mtn je suis perdue
Donc ø^5= ø×ø^4
=ø(3ø+2)=3ø^2+2ø
=3×(ø+1)+2ø
=3ø+3+2ø
=5ø+3
???
Mais avant je voyais la récurrence a faire dans la prochaine question mais mtn je suis perdue
Re: Suites Ts
Oui, c'est ça :
ø^2 = ø + 1
ø^3 = 2ø + 1
ø^4 = 3ø + 2
ø^5 = 5ø + 3
ø^6 = 8ø + 5
ø^7 =13ø + 8
ø^8 =21ø + 13
Et si tu doit faire un lien avec quelque chose, ben ça serait pas bête de calculer les premiers termes de ta fameuse suite_{n\geq 0}) définie par
définie par  puis
puis  pour
pour 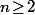 .
.
ø^2 = ø + 1
ø^3 = 2ø + 1
ø^4 = 3ø + 2
ø^5 = 5ø + 3
ø^6 = 8ø + 5
ø^7 =13ø + 8
ø^8 =21ø + 13
Et si tu doit faire un lien avec quelque chose, ben ça serait pas bête de calculer les premiers termes de ta fameuse suite
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
