Exercice de somme de suite
19 messages
- Page 1 sur 1
Exercice de somme de suite
Donc voilà, je ne sais vraiment pas par où commencer dans cet exercice, de plus j'ai beaucoup de mal avec la notation sigma de la somme..
Voici l'énoncé :
On considère la suite (Un) définie pour tout n qui appartient à IN par Un = 5 × 2^n + 4n - 1
Montrer que n
Σ Uk=5(2^n+1 -1)+(n + 1)(2n -1)
k=0
Désolé je n'ai pas pu noter ça autrement, le n est au dessus du sigma et le k=0 en dessous, et le 2^n+1 c'est bien tout le n+1 qui est en explosant, n+1 étant bien le terme suivant n, histoire d'être bien comprise :)
Voici l'énoncé :
On considère la suite (Un) définie pour tout n qui appartient à IN par Un = 5 × 2^n + 4n - 1
Montrer que n
Σ Uk=5(2^n+1 -1)+(n + 1)(2n -1)
k=0
Désolé je n'ai pas pu noter ça autrement, le n est au dessus du sigma et le k=0 en dessous, et le 2^n+1 c'est bien tout le n+1 qui est en explosant, n+1 étant bien le terme suivant n, histoire d'être bien comprise :)
Re: Exercice de somme de suite
la somme des Uk de 0 à n est : U0+U1+...+Un. (sigma est une notation pour éviter d'énumérer les termes, ça aère plus la formulation. Toutefois, il peut être bon de l'écrire en énumérant ces termes pour 'voir' quelque chose que l'on aurait pas vu sinon, mais ce n'est pas la question).
Tu as du apprendre un raisonnement pour vérifier si une propriété qui dépend d'un paramètre n est vraie, utilises-la et go !
Tu as du apprendre un raisonnement pour vérifier si une propriété qui dépend d'un paramètre n est vraie, utilises-la et go !
Re: Exercice de somme de suite
Salut,
On peut aussi directement calculer la somme sans faire de récurrence vu qu'elle est composée d'un truc de la forme 1+q+q^2+...+q^n et d'un autre de la forme 1+2+3+...+n et qu'on connais très bien les deux sommes en question.
On peut aussi directement calculer la somme sans faire de récurrence vu qu'elle est composée d'un truc de la forme 1+q+q^2+...+q^n et d'un autre de la forme 1+2+3+...+n et qu'on connais très bien les deux sommes en question.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Exercice de somme de suite
Je n'ai pas très bien compris ou vous vouliez en venir. Il a deux formes ?
Re: Exercice de somme de suite
Qaterio, je ne vois pas comment procéder avec la récurrence (je ne vois que cette propriété )
Re: Exercice de somme de suite
Montrons que
(Σ Uk jusquà n+1) -(Σ Uk jusquà n)=Un+1
et que c'est vrai pour n=0
variante :
Σ1 de 0 à n = n+1
Σn de 0 à n = n(n+1)/2
Σn² de 0 à n = n(n+1)(2n+1)/6
(Σ Uk jusquà n+1) -(Σ Uk jusquà n)=Un+1
et que c'est vrai pour n=0
variante :
Σ1 de 0 à n = n+1
Σn de 0 à n = n(n+1)/2
Σn² de 0 à n = n(n+1)(2n+1)/6
Re: Exercice de somme de suite
Je n'ai vraiment pas compris ce que vous avez écrit, pouvez vous m'expliquer ? Merci
Re: Exercice de somme de suite
Un = 5 × 2^n + 4n - 1
So=Σ1 de 0 à n = n+1
S1=Σn de 0 à n = n(n+1)/2
S2= Σn² de 0 à n = n(n+1)(2n+1)/6
ΣUn = 5 × S2 + 4S1 - S0
aller plus loin, c'est t'écrire la réponse, faut pas pousser
variante, sauf erreur de calcul, on fait moins de faute écrit à la main
Σ Uk=5(2^(n+1) -1)+(n + 1)(2n -1)
Σ^(n+1) - Σ^(n)= 5(2^(n+1+1) -1)+(n + 1+1)(2n+2 -1)-[5(2^(n+1) -1)+(n + 1)(2n -1)]
(double distributivité vu au collège, conformée au lycée)
= 5(2 *2^(n+1) -1) + (n + 1)(2n-1) +(2n-1) + (n+1)(2)+1(2) -[5(2^(n+1) -1)+(n + 1)(2n -1)]
= 5 *2^(n+1)+(2n-1) + (n+1)(2)+1(2)
= presque fini, un "-" s'est peut-être égaré et il faut regrouper 4n en 4(n+1)-...
So=Σ1 de 0 à n = n+1
S1=Σn de 0 à n = n(n+1)/2
S2= Σn² de 0 à n = n(n+1)(2n+1)/6
ΣUn = 5 × S2 + 4S1 - S0
aller plus loin, c'est t'écrire la réponse, faut pas pousser
variante, sauf erreur de calcul, on fait moins de faute écrit à la main
Σ Uk=5(2^(n+1) -1)+(n + 1)(2n -1)
Σ^(n+1) - Σ^(n)= 5(2^(n+1+1) -1)+(n + 1+1)(2n+2 -1)-[5(2^(n+1) -1)+(n + 1)(2n -1)]
(double distributivité vu au collège, conformée au lycée)
= 5(2 *2^(n+1) -1) + (n + 1)(2n-1) +(2n-1) + (n+1)(2)+1(2) -[5(2^(n+1) -1)+(n + 1)(2n -1)]
= 5 *2^(n+1)+(2n-1) + (n+1)(2)+1(2)
= presque fini, un "-" s'est peut-être égaré et il faut regrouper 4n en 4(n+1)-...
Re: Exercice de somme de suite
c'est marrant, je voulais écrire confirmée et (c'est pas moi, c'est mon clavier sans qui a été victime d'une interférence) il est apparu conformée qui est tout à fait valable.
Au niveau difficulté de l'exo, au lycée, Σ met un peu de temps à bien être compris et pour une fois, les probas aident bien. Si le prof demande ce niveau, c'est soit de la recherche soit une continuité de ce qui a été déjà fait, donc faisable.
Au niveau difficulté de l'exo, au lycée, Σ met un peu de temps à bien être compris et pour une fois, les probas aident bien. Si le prof demande ce niveau, c'est soit de la recherche soit une continuité de ce qui a été déjà fait, donc faisable.
Re: Exercice de somme de suite
Mais en fait je ne comprends vraiment pas les trois premières lignes de votre explication, d'où êtes vous parti, c'est simplement ce que je demandais. Je ne comprends pas pq la somme de o à n est égale à n, ni pourquoi vous avez écrit sigma1
Re: Exercice de somme de suite
Pouvez vous développer votre explication, je n'ai en aucun cas demander les réponses, et s'il vous plait ne soyez pas désagréable.
Re: Exercice de somme de suite
Uk=5.2^k+4k-1.
Tu peux écrire ça sous la forme de trois séries (sigma) dont tu connais les valeurs générales. Comme l'a dit @Ben314. Ou bien alors si tu n'y arrives vraiment pas comme ça. Tu fais un raisonnement par récurrence.
Tu peux écrire ça sous la forme de trois séries (sigma) dont tu connais les valeurs générales. Comme l'a dit @Ben314. Ou bien alors si tu n'y arrives vraiment pas comme ça. Tu fais un raisonnement par récurrence.
Re: Exercice de somme de suite
Bonjour
D'abord, sauf erreur, je n'ai vu personne de désagréable.
Mis à part cela je fais un résumé des différentes remarques:
Tu as une expression de en fonction de n.
en fonction de n.
Et puis on te demande de montrer que
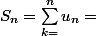 quelque chose en "fonction de n." que je note f(n).
quelque chose en "fonction de n." que je note f(n).
Pour le démontrer il y a l'option évidente de faire une démo par récurrence.
Néanmoins quelqu'un qui a une certaine vision des mathématiques voit que: on aurait pu voir par soi même ce qu'est la fonction de n (cf message de @ben).
Donc pour toi progresser il serait bien que tu vois les 2 démo.
Commençons par la récurrence:
Pour n=0 c'est évident ( à faire)
Supposons que pour un entier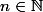 , on a
, on a 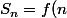)
Il faut démontrer que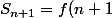) .
.
On te fait remarque que
Donc par hypothèse de récurrence on a :
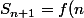+u_{n+1})
Il reste donc à calculer+u_{n+1}) et montrer que c'est égal à f(n+1).
et montrer que c'est égal à f(n+1).
Peux-tu le faire?
Deuxième méthode. On calcule nous même l'expression de f(n):
On a
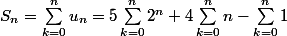
Mais c'est une somme d'une suite géométrique (connu, tu peux le faire?)
c'est une somme d'une suite géométrique (connu, tu peux le faire?)
Mais ( hyper connu, voir Gauss )
( hyper connu, voir Gauss )
 (facile)
(facile)
Tu peux finir s-t-p
D'abord, sauf erreur, je n'ai vu personne de désagréable.
Mis à part cela je fais un résumé des différentes remarques:
Tu as une expression de
Et puis on te demande de montrer que
Pour le démontrer il y a l'option évidente de faire une démo par récurrence.
Néanmoins quelqu'un qui a une certaine vision des mathématiques voit que: on aurait pu voir par soi même ce qu'est la fonction de n (cf message de @ben).
Donc pour toi progresser il serait bien que tu vois les 2 démo.
Commençons par la récurrence:
Pour n=0 c'est évident ( à faire)
Supposons que pour un entier
Il faut démontrer que
On te fait remarque que
Donc par hypothèse de récurrence on a :
Il reste donc à calculer
Peux-tu le faire?
Deuxième méthode. On calcule nous même l'expression de f(n):
On a
Mais
Mais
Tu peux finir s-t-p
Modifié en dernier par aviateur le 29 Sep 2018, 10:55, modifié 2 fois.
Re: Exercice de somme de suite
Je ne comprends vraiment rien, j'aimerai juste comprendre par où commencer, quelle expression prendre ? Et pour la récurrence quel rang n veut on prouver ?
Re: Exercice de somme de suite
Bonjour
Alors pour commencer, on va simplement faire la démonstration par récurrence.
Tu démontres tout simplement que la propriété est vrai pour n=0.
Alors pour commencer, on va simplement faire la démonstration par récurrence.
Tu démontres tout simplement que la propriété est vrai pour n=0.
Re: Exercice de somme de suite
Et c'est là somme de Uk qu'on cherche, pourquoi on fait des sommes avec 1,2 et 3
Re: Exercice de somme de suite
Le deux premières sommes sont connues :
pour i allant de 0 à n
Σ1 = 1 + 1+....+1 = n+1
pour i allant de 0 à n
Σi = 1 + 2+3+....+n = n(n+1)/2
pour i allant de 0 à n
Σ1 = 1 + 1+....+1 = n+1
pour i allant de 0 à n
Σi = 1 + 2+3+....+n = n(n+1)/2
Re: Exercice de somme de suite
Maylisttt a écrit:Et c'est là somme de Uk qu'on cherche, pourquoi on fait des sommes avec 1,2 et 3
k est l'indice de la somme, il varie de 0 à n d'après ton énoncé
la somme des Uk pour k variant de 0 à n est égale à U0 + U1 + U2 + ... + Un
Un = 5 × 2^n + 4n - 1
exemple avec n = 3
k varie de 0 à 3
(correspondant à la 2eme méthode du post d'aviateur de 11:37)
U0 = 5 × 2^0 + 4 x 0 - 1
U1 = 5 × 2^1 + 4 x 1 - 1
U2 = 5 × 2^2 + 4 x 2 - 1
U3 = 5 × 2^3 + 4 x 3 - 1
pour simplifier le calcul de la somme S = U0 + U1 + U2 + U3 on peut regrouper les termes en 5 x 2^k puis les termes en 4 x k puis les termes -1
cela donne :
S = (5 × 2^0 + 5 × 2^1 + 5 × 2^2 + 5 × 2^3) + (4 x 0 + 4 x 1 + 4 x 2 + 4 x 3) -1 -1 -1 -1
en mettant en facteur les constantes :
S = 5 x (2^0 + 2^1 + 2^2 + 2^3) + 4 x (0 + 1 + 2 + 3) + (-1) x 4
or tu sais calculer directement 2^0 + 2^1 + 2^2 + 2^3 car c'est une suite géométrique de raison 2
de meme 0 + 1 + 2 + 3 est une suite arithmétique de raison 1
en extrapolant pour n quelconque, tu devrais obtenir les formules de l'énoncé
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 183 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
