Geometrie

[Antoine1998]

Bonjour, j'aimerai savoir comment procéder pour trouver une equation d'une droite à l'aide d'un point et un vecteur directeur. ( Question a)

[pascal16]

la droite est l'ensemble des point de coordonnées A+vt, avec t, nombre réel
soit le système
x=2-t
y=-1+2t
z=3-t

les équation paramétriques sont toutes de la forme (mais c'est pas demandé en lycée)
x=(2-k)-ut
y=(-1+2k)+2ut
z=(3-k)-ut
avec k réel (fixe un point de départ), u réel non nul (est un vecteur directeur) et t réel (est le paramètre)
elle se ramènent toute à la première donnée.


Les équation cartésiennes, c'est plus dur, il faut choisir au hasard deux plans qui se coupent sur la droite, et, niveau lycée sans produit vectoriel, c'est laborieux. On te donne quoi comme explication à suivre ?

[mathelot]

bonjour,
soit (R) un repère de l'espace.
l'équation de la droite D passant par de vecteur directeur
est

[titine]

........

[mathelot]

pour l'équation cartésienne de (D),
on calcule le paramètre t de deux manières




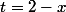
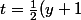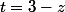
soi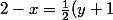t et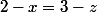

(D) est donc à l'intersection des deux plans d'équation
2x+y-3=0
x-z+1=0

ces deux dernières égalités constituent une équation cartésienne de (D)

[pascal16]

Il faut en trouver plusieurs, en éliminant t entre deux autres équations, tu as un autre plan. Soit au final 3 choix d’intersection de deux plans (1-2, 2-3 et 3-1)

[Antoine1998]

Merci pour vos réponses