Valeur propre

[pffffffffff]

Bonjour,

Dans un exercice, on me demande de justifier que est une valeur propre de si et seulement si .

Je sais qu'on appelle valeur propre d'un endomorphisme , un réel telqu'il existe un vecteur u non nul tel que
mais je ne vois pas le rapprochement avec le noyau...

merci

[Ben314]

Salut,
C'est quoi la définition du noyau d'un endomorphisme ?
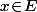
Et ça veut dire quoi (par définition) qu'un vecteur est dans la noyau de l'endomorphisme ?

[pffffffffff]

Dans ce cas le noyau c'est les antécédents de dans E

Ça veut dire que le noyau de n est pas nulle, donc l'endomorphisme est non injectif donc Ker () n'est pas réduit à vecteur nulle et si je remplace dans votre "énoncé" x par , la justification est suffisante ?

[aviateur]

et si je remplace dans votre "énoncé" x par , la justification est suffisante ?

Bonjour
ça pose problème. Pour @ben x est un vecteur et est un scalaire.
C'est deux choses de natures différentes

[pffffffffff]

Le vecteur u serait plus convenable alors

[aviateur]

pas du tout. Tout ce que tu as dis est correct ainsi que @ben dans sa réponse?
But infortunatelly, la partie de ce que tu dis et que j'ai soulignée pose problème (dans ta compréhension)

[pffffffffff]

oui

[pffffffffff]

Ce que je dis n'est pas correct alors...

[aviateur]

Je ne sais pas mais raisonne s-t-p:

est vecteur propre de pour la valeur propre signifie que ... et puis on continue sans confondre et
qui sont de natures différentes.

[pffffffffff]

Oui mais avec l'énoncé que j'ai, je peux prendre le vecteur u comme vecteur propre de de telle sorte que et donc dire que u est dans le noyau de l'endomorphisme

Merci pour les explications

[Sylviel]

Oui, il faut écrire proprement les choses.

Soit un vecteur propre de associé à la valeur propre .
On a que
ou encore
ou encore
et donc .

Maintenant tu écris la réciproque : soit non nul, montrons qu'il s'agit d'un vecteur propre de \varphi.
A toi.