Comment résoudre cette équation
(1+z^2)^3 = (1-z^2)^3
Équation dans les complexes
7 messages
- Page 1 sur 1
Re: Équation dans les complexes
une façon de faire est de résoudre a³ = b³.
ça va te donner 3 équations ou 1 seule avec un modulo différent de 2pi
ensuite on remonte
a=1+z², b =1-z²
sans doute encore 2 solutions à chaque fois.
ça va te donner 3 équations ou 1 seule avec un modulo différent de 2pi
ensuite on remonte
a=1+z², b =1-z²
sans doute encore 2 solutions à chaque fois.
Re: Équation dans les complexes
Bonjour
Il y a surement plusieurs façon d'attaquer le sujet mais l'équation étant polynomiale et 0 étant solution évidente, il serait peut être judicieux d'en tenir compte pour la rendre + simple i.e
on a (1+z^2)^3-(1-z^2)^3=0 soit 2 z^2(z^4+3)=0.
D'où 0 solution double et les 4 racines quatrième de -3.
Il y a surement plusieurs façon d'attaquer le sujet mais l'équation étant polynomiale et 0 étant solution évidente, il serait peut être judicieux d'en tenir compte pour la rendre + simple i.e
on a (1+z^2)^3-(1-z^2)^3=0 soit 2 z^2(z^4+3)=0.
D'où 0 solution double et les 4 racines quatrième de -3.
Re: Équation dans les complexes
Salut !
Une autre manière de faire : -1 et 1 ne sont clairement pas solution de l'équation donc résoudre^3 = (1-z^2)^3) équivaut à résoudre
équivaut à résoudre  en posant
en posant 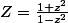 .
.

Theo07170 a écrit:Comment résoudre cette équation
(1+z^2)^3 = (1-z^2)^3
Une autre manière de faire : -1 et 1 ne sont clairement pas solution de l'équation donc résoudre
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Équation dans les complexes
Oui, pour toute ces indication,
mais faire comme j'ai fait donne directement toutes les solutions.
Pour mémoire les racines 4ème de (-1) sont bien connues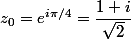
 d'où les racines 4ème de -3 directement.
d'où les racines 4ème de -3 directement.
mais faire comme j'ai fait donne directement toutes les solutions.
Pour mémoire les racines 4ème de (-1) sont bien connues
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
