Bonjour, je suis actuellement en train de faire mon devoir maison mais je suis bloqué dès la première question, je vous écris la consigne et la question,
On considère la fonction f définie par f(x)=4x²+16x-9
1- Sur quel ensemble est définie f?
Merci de votre futur aide
Une étude de fonction
11 messages
- Page 1 sur 1
Re: Une étude de fonction
bjr
L'ensemble ou domaine de définition d'une fonction ƒ est l'ensemble de tous les réels x pour lesquels ƒ(x) existe ou est calculable. On le note Df . Lorsqu'on étudie une fonction, il est nécessaire de donner d'abord son domaine de définition. On peut alors l'étudier sur tout intervalle I contenu dans D
pour une fonction polynôme, sans racine ni inconnue en position de dénominateur, le domaine de définition est l'ensemble des réels, soit l'ensemble R
https://www.dcode.fr/domaine-definition-fonction
https://www.youtube.com/watch?v=DfA65dS9Urw
L'ensemble ou domaine de définition d'une fonction ƒ est l'ensemble de tous les réels x pour lesquels ƒ(x) existe ou est calculable. On le note Df . Lorsqu'on étudie une fonction, il est nécessaire de donner d'abord son domaine de définition. On peut alors l'étudier sur tout intervalle I contenu dans D
pour une fonction polynôme, sans racine ni inconnue en position de dénominateur, le domaine de définition est l'ensemble des réels, soit l'ensemble R
https://www.dcode.fr/domaine-definition-fonction
https://www.youtube.com/watch?v=DfA65dS9Urw
Re: Une étude de fonction
Non. Je n'arrive pas non plus à comprendre commen on peux faire un encadrement de f(x)=4x²+16x-9 avec 3inferieur stric à x inferieur stric a 10 Pouvez vous m'expliquer, je ferais les autre encadrement seul.
Modifié en dernier par MatAmb le 25 Avr 2018, 10:41, modifié 1 fois.
Re: Une étude de fonction
Salut !
Etant donnée une fonction quelconque , ce qu'on appelle le domaine de définition de
, ce qu'on appelle le domaine de définition de  , noté
, noté  en général, c'est l'ensemble des réels
en général, c'est l'ensemble des réels  pour lesquels l'expression
pour lesquels l'expression ) définissant la fonction
définissant la fonction  a un sens (ou existe si tu préfères).
a un sens (ou existe si tu préfères).
Par exemple, la fonction définie par
définie par =\frac{1}{x-1}) est définie si et seulement si
est définie si et seulement si  (car on ne peut pas diviser par
(car on ne peut pas diviser par  ). Cela revient à dire que
). Cela revient à dire que  . Ainsi le domaine de définition de
. Ainsi le domaine de définition de  est
est  . Autre exemple, la fonction
. Autre exemple, la fonction  définie par
définie par =\sqrt{2-x}) est définie si et seulement si
est définie si et seulement si  (car on ne peut pas prendre la racine carré d'un nombre négatif) donc
(car on ne peut pas prendre la racine carré d'un nombre négatif) donc  .
.
Ici, ta fonction est d'un type bien particulier : c'est une fonction polynomiale de degré 2 : c'est-à-dire de la forme=ax^2+bx+c) , avec
, avec  non nul. Une fonction polynomiale est toujours définie sur
non nul. Une fonction polynomiale est toujours définie sur  tout entier.
tout entier.
Etant donnée une fonction quelconque
Par exemple, la fonction
Ici, ta fonction est d'un type bien particulier : c'est une fonction polynomiale de degré 2 : c'est-à-dire de la forme
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Une étude de fonction
Merci, j'ai maintenant compris cela, mais dans mon DM j'ai une question donc avec f(x)=4x²+16x-9, je dois faire un encadrement pour 3inferieur strictement à x inférieur strictment à 10 . Comment dois je faire pour résoudre cela, pouvez vous me donner un exemple.
Re: Une étude de fonction
A partir de l'encadrement  :
:
- encadre ,
,
- encadre , puis
, puis 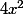 .
.
Déduis-en alors un encadrement de , puis un encadrement de
, puis un encadrement de ) .
.
- encadre
- encadre
Déduis-en alors un encadrement de
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 154 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
