Suites
14 messages
- Page 1 sur 1
Suites
Bonjour, je suis en 1ère L et nous faisons en ce moment le chapitre sur les suites. Nous avons bientôt un DS sur la notion : "sens de variation d'une suite" mais je ne comprends pas tout les procédés qui permettent de trouver le sens de variation. Je sais qu'il faut étudier : u n+1 - u n mais ensuite une fois le résultat trouvé je ne comprends pas comment savoir si la suite est croissante ou décroissante, quelqu'un saurait il m'expliquer?Merci d'avance 
Re: Suites
à n fixé
 est le terme qui suit
est le terme qui suit  dans la suite
dans la suite
exemple : U6 suit U5.
si pour tout n, , ça veut dire que le terme suivant est toujours plus grand, donc la suite est croissante
, ça veut dire que le terme suivant est toujours plus grand, donc la suite est croissante
 s'écrit aussi
s'écrit aussi 
et elle est décroissante si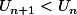 soit
soit 
On étudie donc le signe de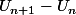
exemple : U6 suit U5.
si pour tout n,
et elle est décroissante si
On étudie donc le signe de
Re: Suites
Dans un exemple je trouve -2n - 1 pour u n+1 - u n , mais comment je sais si u n+1 - u n < 0 ou si
u n + 1 - u n > 0 ?
u n + 1 - u n > 0 ?
Re: Suites
ch09 a écrit:Dans un exemple je trouve -2n - 1 pour u n+1 - u n , mais comment je sais si u n+1 - u n < 0 ou si
u n + 1 - u n > 0 ?
n est un entier , il est positif
on multiplie par -1:
on multiplie par 2 les deux membres de l'inégalité:
on soustraie 1 des deux côtés
on utilise la transitivité de l'inégalité:
Re: Suites
ch09 a écrit:D'accord merci et cette technique s'applique à toutes les suites?
non, pas à toutes les suites
Re: Suites
Nous ne l'avons pas encore abordée en cours, mais que ce soit pour les suites par récurrence ou les autres la méthode reste la même?
Re: Suites
pour les suites définies par récurrence, on a les variations par récurrence.
soit)
si f est croissante sur son domaine, l'inégalité
 est héréditaire en composant par f
est héréditaire en composant par f
soit
si f est croissante sur son domaine, l'inégalité
Re: Suites
Donc la première méthode ne fonctionne que sur les autres suites, par sur celles par récurrence?
Re: Suites
Voici un exercice que l'on n'a pas fait en cours :
" Dans cet exercice, on utilisera la méthode de la différence pour prouver la monotonie des suites :
1) Soit (u n ) n appartenant à N , la suite dont le terme de rang n est définie par : u n = -32n + 102
Montrer que cette suite est décroissante " quelle serait la réponse ?
" Dans cet exercice, on utilisera la méthode de la différence pour prouver la monotonie des suites :
1) Soit (u n ) n appartenant à N , la suite dont le terme de rang n est définie par : u n = -32n + 102
Montrer que cette suite est décroissante " quelle serait la réponse ?
Re: Suites
Ben là c'est évident, à chaque terme tu ôtes 32 au terme précédent.
U(n+1) - Un = -32 ( n+1) + 102 - ( -32 n + 102) = -32n - 32 + 102 + 32n + -102 = - 32
U(n+1) - Un = -32 ( n+1) + 102 - ( -32 n + 102) = -32n - 32 + 102 + 32n + -102 = - 32
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
