Nombres complexes
15 messages
- Page 1 sur 1
Nombres complexes
Bonjour.
Pourriez vous m'aider svp?
Exo:
Mettre chaque nombre complexe suivant sous forme trigonométrique puis sois forme algébrique:
à) (-1+i)^5
b) (3 - i)^4
c) (1+ i3 )^3
d) (2i -23 )/(4i+4)
e) (1+ i3 )^7/(1-i3 )^12
Merci bcp
Maria
Pourriez vous m'aider svp?
Exo:
Mettre chaque nombre complexe suivant sous forme trigonométrique puis sois forme algébrique:
à) (-1+i)^5
b) (3 - i)^4
c) (1+ i3 )^3
d) (2i -23 )/(4i+4)
e) (1+ i3 )^7/(1-i3 )^12
Merci bcp
Maria
Re: Nombres complexes
bonjour,
écrire -1+i sous forme trigonométrique puis élever à la puissance 5
sous forme trigonométrique
si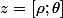 alors
alors 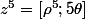
écrire -1+i sous forme trigonométrique puis élever à la puissance 5
sous forme trigonométrique
si
Modifié en dernier par mathelot le 01 Avr 2018, 14:50, modifié 2 fois.
Re: Nombres complexes
Voilà ce que j'ai fait:
Pour forme trigo:
Je cherche le module:
l z l = (racine de 2)^5 = 5,65 ?
Ça m'a l'air faux...
Pourquoi est-ce que je dois enlever la puissance ?
Pour forme trigo:
Je cherche le module:
l z l = (racine de 2)^5 = 5,65 ?
Ça m'a l'air faux...
Pourquoi est-ce que je dois enlever la puissance ?
Re: Nombres complexes
Daccord mais dans la formule que vous avez ecrit,
Que signifie le p devant le cos et sin ?
Que signifie le p devant le cos et sin ?
Re: Nombres complexes
sweetassbaby a écrit:Daccord mais dans la formule que vous avez ecrit,
Que signifie le p devant le cos et sin ?
c'est le module de -1+i
Re: Nombres complexes
Daccord merci bcp.
J'ai pu réussir la à) b) et c)
Pour la d) la je bloque car je veux écrire le cos Alpha et et le sin Alpha sauf que c'est un quotient je ne sais pas qui est le a et et qui est le b ?
J'ai pu réussir la à) b) et c)
Pour la d) la je bloque car je veux écrire le cos Alpha et et le sin Alpha sauf que c'est un quotient je ne sais pas qui est le a et et qui est le b ?
Re: Nombres complexes
sweetassbaby a écrit:d) (2i -23 )/(4i+4)
e) (1+ i3 )^7/(1-i3 )^12
pour la (d), factorise 4 au dénominateur.
le dénominateur devient 4(1+i)
Multiplie le quotient haut et bas par la quantité conjuguée de 1+i,soit 1-i:
son dénominateur devient 4(1+i)(1-i)=8
Re: Nombres complexes
explication: quand on montre que le nombre non nul a+bi possède un inverse,
on écrit
déf: a+bi et a-bi sont deux quantités "conjuguées". leur produit est un réel positif (a,b réels)
Re: Nombres complexes
mince!! Desole ! Je viens de me rendre compte que j'avais omis la racine dans le d)
L'expression au numérateur est 2i - 2racinede3
Desole encore une fois
J'ai trouvé la forme algébrique du nombre complexe, pour la d) je le rappele:
Je trouve;
z = (1-3 )/(4) + (1+3 )/(4) i
Merci
L'expression au numérateur est 2i - 2racinede3
Desole encore une fois
J'ai trouvé la forme algébrique du nombre complexe, pour la d) je le rappele:
Je trouve;
z = (1-3 )/(4) + (1+3 )/(4) i
Merci
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
