*DM maths tangentes

[leabarlet]

BOnjour, besoin d'aide pour un exercice

f est définie sur R-{2} par:

Agnès a tracé la courbe représentative de la fonction f et sa tangente au point d'abscisse -2
Victor affirme qu'elle est parallele a l'axe des abscisses ? est ce vrai?

Je sais quil faut calculer l'equation de la tangente et resoudre un systeme je pense mais je n'arrive pas a calculer l'equation de la tangente

[nodgim]

As tu calculé la dérivée au préalable et quelle est sa valeur en -2 ?

[pascal16]

Je sais quil faut calculer l'equation de la tangente et resoudre un systeme je pense mais je n'arrive pas a calculer l'equation de la tangente

les matheux compliquent les notations sur le tangentes, c'est parfois difficile de ne pas tout confondre.

... tangente au point d'abscisse -2
Victor affirme qu'elle est parallele a l'axe des abscisses

parallele a l'axe des abscisses se traduit directement par f'(-2)=0

on cherche donc on vérifier si f'(-2)=0

1 -> calculer f'(x)
2 -> vérifier si f'(-2)=0

f est du type u/v donc f'= .... d'après le formulaire à apprendre par coeur
avec u=...
v=...
on a u'= .... et v'=...

[mathelot]

f est définie sur R-{2} par:

bonjour,
peux tu parenthéser ? ce qu'il y a écrit vaut
3x+(-5.9/x) -2

[aymanemaysae]

Bonjour ;

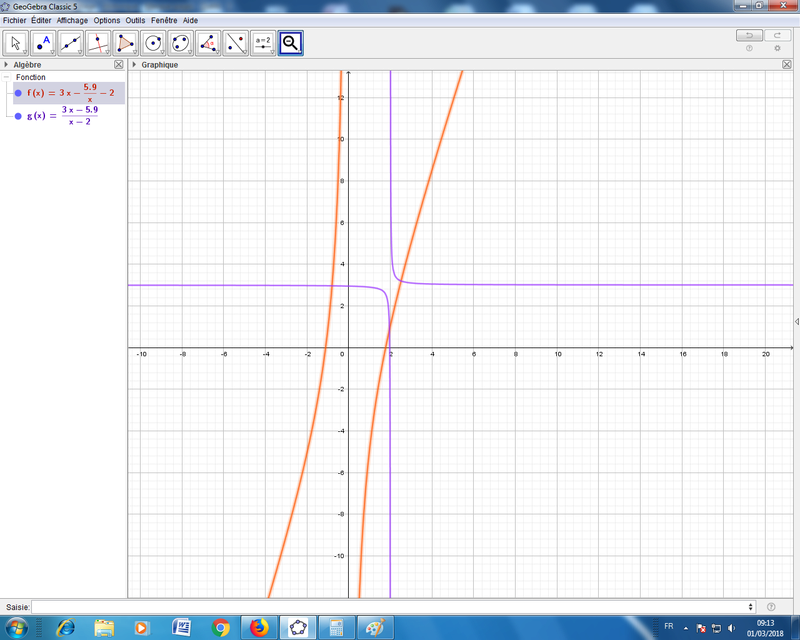
Considérant le fichier ci-dessous , je crois qu'on a :

On a donc :



donc :

Tu peux maintenant trouver l'équation réduite de la tangente à la courbe représentative de f au point d'abscisse x = - 2 et voir si elle est parallèle à l'axe des abscisses .