Matrice valeur propre double

[Moonlight12]

Bonjour,

Je suis actuellement en train de travailler sur les matrices et les conditions pour la diagonaliser. En lisant mon cours, il y'a un point que je n'arrive pas à comprendre... Est ce que quelqu'un pourrait m'éclairer svp ?

Je cite :
"Dans le cas d'une valeur propre réelle double, on recherche Eƛ = {U/AU=ƛU} dim Eƛ ≥ 1.
Soit dim Eƛ =2 l'espace propre associé à la valeur propre double est de dimension 2, la matrice est diagonalisable
Soit dim Eƛ =1 il y a une seule direction propre AU=ƛU, la matrice n'est pas diagonalisable mais triangularisable dans ℝ"

Je vous remercie d'avance,

[aviateur]

Bonjour
C'est tout de même bizarre ta question. En effet on ne sait même pas si ta matrice est de taille 2 ou plus, on a l'impression que c'est à nous de mettre les hypothèses qui vont bien.
On peut ne pas comprendre certaines notions mais au moins on doit comprendre qu'une question doit être formulée correctement.
Précises donc le contexte s-t-p

[Moonlight12]

On se situe sur une matrice d'ordre 2, où :
ƛ est dite valeur propre double de la matrice A si PA(λ) se factorise par (ƛ-λ)^2
ƛ est dite valeur propre triple de A si PA(λ) se factorise par (ƛ-λ)^3
ƛ valeur propre de multiplicité d'ordre m, si PA(λ) se factorise par (ƛ-λ)^m

La question est : pour ƛ valeur propre multiple d'ordre m, a-t-on E1 de dimension de m ?

On se sert du coup du discriminant, et on note trois cas de figure :

Δ>0 : il y'a deux valeurs propres réelle distinctes et donc deux vecteur propres non liés, donc A est diagonalisable.
Δ=0 : il y a une valeur propre réelle double. Ou bien elle est diagonalisable, ou bien elle est triangularisable, et cela dépend des conditions que j'ai cité dans le premier message, que je n'arrive pas a éclaircir...
Δ<0 : et là, on doit se placer dans le système des complexes.

J'espère avoir restituer le contexte correctement et que cela répond à vos attentes...

[Pseuda]

Bonsoir,

Quelle est la question ? Tu y as répondu : si le polynôme caractéristique a une racine double , alors la matrice est diagonalisable ssi l'espace prore associé à la valeur propre est de dimension 2 (c'est-à-dire qu'il existe une base de vecteurs propres), sinon il est de dimension 1, et la matrice n'est que trigonalisable (polynôme scindé).

[aviateur]

Mes attentes c'est de comprendre la question pour pouvoir y répondre!
Donc on est avec une matrice carrée réelle d'ordre 2 avec valeur propre double.
J'appelle A cette matrice.

Premier cas le sous espace propre est de dimension 2. Alors A est bien diagonalisable. Et pourquoi?
parce que A est déjà une matrice diagonale!!!


Deuxième cas Le sous espace propre est de dimension 1. Alors A n'est pas diagonalisable.
En effet si elle l'était, elle serait semblable à la matrice diagonale ( 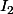matrice identité). C'est à dire qu'il existerait une matrice P inversible telle que
donc imp.

Mais si un vecteur directeur du sous-espace propre. On complète par n'importe quel vecteur 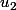de sorte que forment un base. Alors la matrice P =(u_1|u_2) est inversible et
est triangulaire supérieure avec des dans la diagonale.


Comme exemple tu peux considérer la matrice qui n'est pas diagonalisable quelle soit la valeur de a.

[Moonlight12]

Merci beaucoup, je pense avoir compris maintenant !! J'ai appliqué toute l'après midi, et votre explication renforce le fait que c'est bien plus clair dans mon esprit.

Merci encore ! Passez une bonne soirée