merci d'avance
Suites
8 messages
- Page 1 sur 1
suites
bonsoir svp j'ai une question voila lorsqu'on nous demande d'etudier la convergence d'une suite comment proceder ? d'ou debuter ?
merci d'avance
merci d'avance
Re: suites
on prends la calculette ou le tableur, on regarde la tendance, si la suite croit ou pas, si elle semble tendre vers une limite ou diverger.
ensuite : on démontre chaque supposition.
Bien sur, on connait les croissances comparées et autres résultats sur les suites qui permettent de ne pas repartir à 0 à chaque fois
as-tu quelques suites sous la main ?
ensuite : on démontre chaque supposition.
Bien sur, on connait les croissances comparées et autres résultats sur les suites qui permettent de ne pas repartir à 0 à chaque fois
as-tu quelques suites sous la main ?
Re: suites
pascal16 a écrit:on prends la calculette ou le tableur, on regarde la tendance, si la suite croit ou pas, si elle semble tendre vers une limite ou diverger.
ensuite : on démontre chaque supposition.
Bien sur, on connait les croissances comparées et autres résultats sur les suites qui permettent de ne pas repartir à 0 à chaque fois
as-tu quelques suites sous la main ?
dacc merci oui en fait , il y'a une suite sur laquelle je me bloque c'est cos(na) sachant que a appartient a R\piZ puisque on nous a demander de raisonner par absurde en considerant ( u(n+2)-u(n)) et (u(n+2)+u(n)) je sais pas comment proceder si vous avez une idee merci de bien vouloir la partager avec moi
Re: suites
posté il y a peu des questions même genre
superieur/limite-exp-pie-t189341.html
en gros si a est du type k.pi -> on peut tomber sur une limite
si a est du type k.pi/d -> la suite ne prend qu'un nombre fini de valeurs
sinon, les valeurs oscillent entre -1 et 1 et aucune limite n'est possible.
je pense qu'il faut d'un coté faire une composition de limite et de l'autre développer le cos(a+b)
superieur/limite-exp-pie-t189341.html
en gros si a est du type k.pi -> on peut tomber sur une limite
si a est du type k.pi/d -> la suite ne prend qu'un nombre fini de valeurs
sinon, les valeurs oscillent entre -1 et 1 et aucune limite n'est possible.
je pense qu'il faut d'un coté faire une composition de limite et de l'autre développer le cos(a+b)
Re: suites
Bonsoir !
Si la suite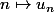 a une limite
a une limite  , la suite
, la suite  converge vers 0.
converge vers 0.
Tu trouves alors que la suitea) est convergente et en calculant
est convergente et en calculant a-\sin(na)) tu verras une contradiction.
tu verras une contradiction.
Si la suite
Tu trouves alors que la suite
Re: suites
Kolis a écrit:Bonsoir !
Si la suitea une limite
, la suite
converge vers 0.
Tu trouves alors que la suiteest convergente et en calculant
tu verras une contradiction.
Bonsoir tu veux dire cos ? Parceque j'arrive pas a aboutir a sin (n+1)a
Modifié en dernier par kousuke le 04 Nov 2017, 00:04, modifié 1 fois.
Re: suites
pascal16 a écrit:posté il y a peu des questions même genre
superieur/limite-exp-pie-t189341.html
en gros si a est du type k.pi -> on peut tomber sur une limite
si a est du type k.pi/d -> la suite ne prend qu'un nombre fini de valeurs
sinon, les valeurs oscillent entre -1 et 1 et aucune limite n'est possible.
je pense qu'il faut d'un coté faire une composition de limite et de l'autre développer le cos(a+b)
mais il est cité dans l'énoncé que a € R\piZ donc il ne peut pas etre du type kpi
Re: suites
Bonsoir tu veux dire cos ? Parceque j'arrive pas a aboutir a sin (n+1)a
Si tu veux faire cet exercice sans connaître tes formules de trigonométrie, je n'y peux rien !
Revois en particulier
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
