Carré parfait

par **aviateurpilot** » 22 Oct 2006, 15:24

salut les amis
voila un probleme facile pour vous

montrer que:

,

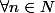
est un carré parfait =>

bon chance

par **yos** » 24 Oct 2006, 15:28

Tu veux dire :

, (

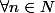
est un carré parfait =>

)?
ou bien :
(

,

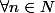
est un carré parfait) =>

?

Je penche pour la seconde.

par **katrena99** » 24 Oct 2006, 22:06

c'est à dire ??? détaillez s'il vous plaît !

par **aviateurpilot** » 24 Oct 2006, 22:33

pour la premiere,
il est clair que c'est faut
car pour

et

,

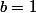
et

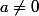
c'est la seconde yos
(

)

par **aviateurpilot** » 25 Oct 2006, 16:57

voila ma solution(pour ceux qui voulent chercher encor,vous n'etes pas obligé de voir ma solution)

soit

on pose

l'equation

=>

est fini
on a

est inclu dans

donc

est fini
=> il existe

tel que

=>

par **BancH** » 27 Oct 2006, 23:26

yos a écrit:Tu veux dire :
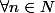
, ( est un carré parfait => )?
ou bien :
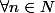
(, est un carré parfait) => ?

Je penche pour la seconde.

C'est quoi vraiment la différence entre les deux là ?
Quelqu'un pourraît m'expliquer ?

par **Zebulon** » 28 Oct 2006, 11:22

BancH a écrit:C'est quoi vraiment la différence entre les deux là ?
Quelqu'un pourraît m'expliquer ?

Bonjour,
la différence, c'est la position du "si" quand on lit cette phrase mathématique en français.
La première est
"pour tout n appartenant à

,
si

est un carré parfait,
alors a=0"
alors que la deuxième est :
"si pour tout n appartenant à

,

est un carré parfait,
alors a=0".

par **BancH** » 28 Oct 2006, 12:10

Merci Zeb, mais je n'arrive vraiment pas à voir la différence...

par **Zebulon** » 28 Oct 2006, 13:18

La première implique la deuxième, mais la réciproque n'est pas vraie.

par **Zebulon** » 28 Oct 2006, 14:01

La contraposée de la deuxième est :
si

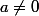
, alors

tel que

n'est pas un carré parfait.
Pour moi, la contraposée de la première est :
pour tout

, si

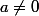
alors

n'est pas un carré parfait, c'est correct?

par **aviateurpilot** » 28 Oct 2006, 14:18

salut banch

; carré parfait =>

on veux montrer que si

sont tous des carré parfait alors a=0

mais pour:

( carré parfait =>

c'est:
si

carré parafait alors

et
si

carré parafait alors

et
si

carré parafait alors

et
si

carré parafait alors

.........
.........
et
si 2

carré parafait alors

.........
.........

par **BancH** » 28 Oct 2006, 16:22

J'ai enfin compris.

Ca veut dire qu'il faut montrer que si

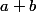
est un carré parfait, alors

n'en est pas un, et par conséquent

est un carré parfait et

.

C'est ça non ?

par **aviateurpilot** » 28 Oct 2006, 16:39

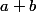
banch a écrit:si est un carré parfait, alors n'en est pas un,

contre-exemple
pour

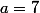
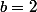
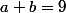
et

.
_______________________
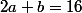
1er methode)essayer de monter que si

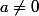
alors il existe surement un k tel que

n'ai pas un carré parfait.

2eme methode)essayer de montrer qu'il n'existe pas une infinité de carré parfait de la forme

c'est ce que j'ai fait dans la solution que j'ai posté.

par **BancH** » 28 Oct 2006, 17:10

Ok, sinon t'as un exemple avec

,

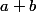
et

carrés parfaits ?

par **aviateurpilot** » 28 Oct 2006, 17:16

tu n'a que voir ma solution,et tu va comprendre tt

Carré parfait

carré parfait

Qui est en ligne