J'écris
Pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
22 messages
- Page 2 sur 2 - 1, 2
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
Deuxieme cas: k+1 n'est pas une puissance de 2
J'écris avec q impair supérieur à 3. Alors j'utilise la factorisation
avec q impair supérieur à 3. Alors j'utilise la factorisation =B(n)C(n)) où
où =\frac{n^q-1}{n-1}=1+n+\cdots+n^{q-1}) et
et =\frac{n^{k+1}-1}{n^q-1}=1+n^q+(n^q)^2+\cdots+(n^q)^{2^{p}-1}) . Pour
. Pour  fixé, soit
fixé, soit  le pgcd de
le pgcd de ) et
et ) . Alors modulo
. Alors modulo  on a
on a =0) donc
donc  et donc
et donc
=1+n^q+(n^q)^2+\cdots+(n^q)^{2^{p}-1}=1+1+\cdots+1=2^q) , donc
, donc  divise
divise  . D'autre part on vérifie que
. D'autre part on vérifie que ) est toujours impair: c'est trivial si n est pair, et si n impair on a modulo 2:
est toujours impair: c'est trivial si n est pair, et si n impair on a modulo 2: =1+\cdots+n^{q-1}=1+\cdots+1=q=1) car q impair. On conclut donc que
car q impair. On conclut donc que 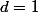 . Ainsi si
. Ainsi si ) est un carré alors
est un carré alors ) (et
(et ) aussi), mais puisque
aussi), mais puisque 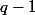 est pair, par le premier cas il n'y a qu'un nombre fini de n tel que
est pair, par le premier cas il n'y a qu'un nombre fini de n tel que ) est un carré.
est un carré.
J'écris
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
Troisieme cas: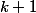 est une puissance de 2
est une puissance de 2
Ecrivons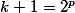 . Je suppose
. Je suppose 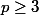 (le cas p=2 correspondant au cas k=3). Alors on a la factorisation
(le cas p=2 correspondant au cas k=3). Alors on a la factorisation =(n+1)(n^2+1)(n^4+1)\cdots(n^{2^{p-1}}+1)) . Le pgcd entre deux différents termes du produit est toujours
. Le pgcd entre deux différents termes du produit est toujours  ou
ou  à cause du fait que si
à cause du fait que si 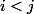 alors
alors  divise
divise  . Donc:
. Donc:
si est pair tous les termes sont premiers entre eux et donc si
est pair tous les termes sont premiers entre eux et donc si ) est un carré, tous les termes sont aussi des carrés: en particulier
est un carré, tous les termes sont aussi des carrés: en particulier 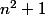 est un carré, ce qui est compliqué...
est un carré, ce qui est compliqué...
si n est impair,alors tous les termes du produit sont pairs, et à part peut être le premier terme tous les termes sont congrus à 2 mod 4. On déduit donc que si
tous les termes sont congrus à 2 mod 4. On déduit donc que si ) est un carré alors tous les termes à part peut être le premier sont de la forme
est un carré alors tous les termes à part peut être le premier sont de la forme  . C'est en particulier le cas pour
. C'est en particulier le cas pour 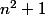 et
et 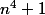 , donc
, donc (n^4+1)) est un carré, et donc en posant
est un carré, et donc en posant 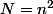 ,
, (N^2+1)=1+N+N^2+N^3) est un carré. On peut donc déduire ce cas du cas
est un carré. On peut donc déduire ce cas du cas 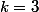
Ecrivons
si
si n est impair,alors tous les termes du produit sont pairs, et à part peut être le premier terme
22 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
