Équation matricielle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Jackza
- Messages: 3
- Enregistré le: 18 Juil 2017, 13:53
-
 par Jackza » 18 Juil 2017, 14:06
par Jackza » 18 Juil 2017, 14:06
Bonjour à tous

Voici l'énoncé : Soit
$)
tel que

,

et

.
1. Montrer que
$)
2. On pose

. Déterminer l'ensemble des matrices M.
Pour la question 1, je n'arrive pas à montrer que M est orthogonale
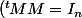)
.
J'essaye de montrer que

mais je n'y arrive pas.
Merci de votre aide.

-
Jackza
- Messages: 3
- Enregistré le: 18 Juil 2017, 13:53
-
 par Jackza » 18 Juil 2017, 19:03
par Jackza » 18 Juil 2017, 19:03
J'ai déjà quelques idées pour la question 2.
On pose :
 = X^{3}-1$)
, un polynôme annulateur de

.
La seule racine possible du polynôme est 1, donc
 \subset \{1\}$)
.
Donc, si

est diagonalisable, elle est semblable à

.
Or, on sait d'après l'énoncé que

.
Ainsi, l'équation n'admet aucune solution si

est diagonalisable.
-
Archytas
- Habitué(e)
- Messages: 1223
- Enregistré le: 19 Fév 2012, 13:29
-
 par Archytas » 18 Juil 2017, 19:34
par Archytas » 18 Juil 2017, 19:34
Jackza a écrit:La seule racine possible du polynôme est 1, donc
 \subset \{1\}$)
.
Attention, tu oublies j e j² donc le polynôme annulateur est scindé à racines simple. M et sa transposée commutent donc sont simultanément diagonalisable. Le problème revient à montrer que 1 est l'unique valeur propre de M ce qui est en contradiction avec le fait que M n'est pas l'identité...
Sauf erreur de ma part une telle matrice n'existe pas. Donc je dois avoir fait une erreur mais je ne vois pas où..
-
Jackza
- Messages: 3
- Enregistré le: 18 Juil 2017, 13:53
-
 par Jackza » 18 Juil 2017, 20:01
par Jackza » 18 Juil 2017, 20:01
Merci de ta réponse, en effet, j'ai oublié j et j².
Dans l'exercice,
)
, donc il me semble cohérent que l'équation n'a pas de solution.
Par contre, je ne vois pas du tout comme faire la quesion 1

-
Archytas
- Habitué(e)
- Messages: 1223
- Enregistré le: 19 Fév 2012, 13:29
-
 par Archytas » 18 Juil 2017, 22:36
par Archytas » 18 Juil 2017, 22:36
Ce que je voulais dire c'est que même la 1/ n'est peut-être pas solvable car aucune matrice ne vérifie ces conditions.
Je m'explique :

implique que

est diagonalisable et par conséquent

l'est aussi.
La relation

implique que

,

sont simultanément diagonalisables (diagonalisable dans une même base). En notant

la matrice de passage on obtient
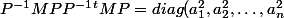(*))
avec

valeurs propres de

donc 1,j ou j².
En supposant que

(ce qu'on doit démontrer), la relation (*) implique
=I)
donc tous les

valent

. Ainsi

est semblable à

, donc
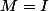
ce qui contredit l'hypothèse de départ.
Je peux me tromper mais à priori il y a une entourloupe dans l'exercice.
Où as-tu trouvé cet exercice ?
-
aviateur
 par aviateur » 18 Juil 2017, 22:48
par aviateur » 18 Juil 2017, 22:48
Bonsoir
M est une matrice à valeurs dans R. Or
^t=M M^t)
est une matrice symétrique donc diagonalisable sur R. ( i.e il existe une b.o.n de vecteurs propres réels et de valeurs propres associées réelles)
Soit dc X un tel vecteur de la b.o.n
On a

avec z dans R.
Maintenant

implique
^3=I)
ainsi
^3=I)
(car
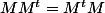)
.
Donc avec le même raisonnement que M on en déduit que les valeurs propres de

sont les racines cubiques de 1 (mais ici réelles) donc z=1. Il vient pour la base b.on

i.e

-
aviateur
 par aviateur » 18 Juil 2017, 22:53
par aviateur » 18 Juil 2017, 22:53
Rebonsoir,
attention messages simultanés.
)
semble être une solution
-
Archytas
- Habitué(e)
- Messages: 1223
- Enregistré le: 19 Fév 2012, 13:29
-
 par Archytas » 19 Juil 2017, 12:14
par Archytas » 19 Juil 2017, 12:14
aviateur a écrit:Rebonsoir,
attention messages simultanés.
)
semble être une solution
Ok, bon je vois où mon raisonnement a merdé : les valeurs propres de la transposée de M sont les conjugués des valeurs propres de M donc la matrice diagonale est bel et bien l'identité, donc pas d'arnaque. Mea culpa.
Désolé pour la fausse piste.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 112 invités
.
semble être une solution