Compensation géométrique

[flamme34kloe]

Bonjour,
Je suis développeuse informatique et je requière votre aide pour mon problème géométrique je m'explique.
Je suis en train de développer une application qui doit piloter des moteurs pour dessiner un motif(à la manière d'une imprimante 3d, sauf que je ne suis qu'en 2D). Je cherche à compenser des défauts de support.
Je dois donc proposer donc à mon utilisateur de faire correspondre 4 points réels sur le support (marque présentes sur le support) avec les 4 points théorique de ces points.

Jusqu'à présent je ne faisais cette compensation que sur 2 points, j'avais donc une rotation, une homothétie et une translation. Mais on me demande de réaliser cette compensation sur 4 point pour compenser des défauts de parallélismes ou de production des supports. Il faut donc que je déforme mon motif de base avec ces transformations à la manière d'une image à laquelle on étire les coins.

je dois écrire un motif sur une surface ou un motif est déjà écrit. il faut donc repositionner le motif en fonction de celui de la surface + compenser les défaut de fabrication de la surface d'origine.

Je joins un exemple par image. la surface de base doit avoir théoriquement un carré de 3.00mm de coté . mais en réalité le motif de la surface est différentes. imaginons a présent que je dois faire un motif a l'intérieur du carré il faut que celui ci s'adapte a la réalité, et se déforme.

compensation.png (29.11 Kio) Vu 408 fois

Pourriez-vous m'aider pour l'aspect mathématique de ce projet ?

[Ben314]

Salut,
Je sais pas quel niveau tu as en mathématique, donc je sais pas si tout ce que je vais raconter sera clair ou pas.
Ton problème, vu sur le plan purement mathématique, ça correspond à trouver un ensemble de "déformations" du plan tel que, étant donné un certain nombre de points "de départs" A1,A2,...,An et le même nombre de points "d'arrivé" B1,B2,...Bn, il y ait une et une seule "déformation" de ton ensemble qui envoie les Ai sur les Bi.

1) Lorsque n=1, le premier ensemble qui vient à l'esprit, c'est celui des translation : étant donné A et B fixés, il y a une unique translation telle que A->B.

2) Lorsque n=2, l'ensemble qui semble le plus simple (et c'est celui que tu avait pris), c'est celui des homothéties+rotations (plus les translations comme cas particulier) : étant donné A1,A2,B1,B2 (*) il y a une unique homothéties+rotations telle que A1->B1 et A2->B2.

3) Lorsque n=3, l'ensemble le plus simple est sans doute celui des applications affines, c'est à dire de la forme (x;y)->(ax+by+c;dx+ey+f) : étant donné A1,A2,A3,B1,B2,B3 (*) il y a une unique application affine telle que A1->B1, A2->B2 et A3->B3.

4) Lorsque n=4, là, à mon avis l'ensemble le plus simple c'est celui des applications projectives (**) c'est à dire de la forme : étant donné A1,A2,A3,A4,B1,B2,B3,B4 (*) il y a une unique application projective telle que A1->B1, A2->B2, A3->B3 et A4->B4.
Si ça te convient comme façon de procéder et que tu n'y arrive pas par toi même, on pourra regarder comment, partant de tes 4 points de contrôle, calculer des valeurs possibles pour les 9 paramètres (***) et/ou comment écrire tes "fonction de transfert" (i.e. coordonnées théorique (x;y) <-> coordonnées à envoyer aux moteurs (x',y') )

(*) Modulo de petites hypothèses sur les différents points.
(**) En rouge, c'est un lien sur l'article de Wiki où tu as un dessin permettant de voir "comment" ça déforme. Il y en a surement pas mal d'autre sur le net pour se faire une idée du type de déformation que ça provoque.
(***) L'application projective est unique, mais pas les paramètres vu que si on les multiplie tous par une même constante, ça donne la même application.

P.S. Pour savoir plus précisément quel serait le "meilleur" type "d'ensemble de déformation" à utiliser, il faudrait savoir plus précisément en quoi consiste les défauts de parallélisme du plan sur lequel tu trace. Mais, à priori, j'aurais tendance à penser que c'est bien ce type là de "déformations" (i.e. les applications projectives) qui correspond le mieux à ton problème.

[flamme34kloe]

Tout d'abord merci d'avoir pris le temps de répondre.

4) Lorsque n=4, là, à mon avis l'ensemble le plus simple c'est celui des applications projectives (**) c'est à dire de la forme : étant donné A1,A2,A3,A4,B1,B2,B3,B4 (*) il y a une unique application projective telle que A1->B1, A2->B2, A3->B3 et A4->B4.
Si ça te convient comme façon de procéder et que tu n'y arrive pas par toi même, on pourra regarder comment, partant de tes 4 points de contrôle, calculer des valeurs possibles pour les 9 paramètres (***) et/ou comment écrire tes "fonction de transfert" (i.e. coordonnées théorique (x;y) <-> coordonnées à envoyer aux moteurs (x',y') )

Cela semble en effet correspondre à mon besoin. je veux bien que tu m'explique comment calculer les paramètre de a à i pour ensuite pour tout point Am à déplacer selon cette règle pouvoir récupérer un point Bm compensé.

P.S. Pour savoir plus précisément quel serait le "meilleur" type "d'ensemble de déformation" à utiliser, il faudrait savoir plus précisément en quoi consiste les défauts de parallélisme du plan sur lequel tu trace. Mais, à priori, j'aurais tendance à penser que c'est bien ce type là de "déformations" (i.e. les applications projectives) qui correspond le mieux à ton problème.

Ces surfaces étant fabriqué par d'autre personnes il arrive que les points réels ne correspondent pas avec la théorie du motif. ces défaut sont minimes et passe les critère de tolérance de notre fournisseur, cela se compte en micromètre mais pour notre application cela peut être suffisant pour nous gêner.

Pour donné un exemple un peu concret de notre application c'est comme si un fournisseur nous envoyait une plaque de circuit imprimé pré percé et que notre équipement devait faire les pistes électronique. si les trou ne sont pas au bon endroit il faut pouvoir compenser cette erreur pour que la piste passe par les trous.

[Ben314]

Concernant le "type de déformation" de toute façon, j'ai dit ça juste par "acquis de conscience" vu qu'au fond, comme "ensemble de déplacement", je sais pas trop quoi te proposer d'autre que l'ensemble des applications projectives.

Sinon, concernant les calculs, tu as plus qu'intérêt à avoir (ou a te faire) une petite bibliothèque de calcul matriciel permettant de faire des produits de matrices 3x3, des produits matrice par vecteur et surtout de calcul d'inverse de matrice 3x3. On peut évidement faire sans, mais ça va faire des formules à rallonges dans lesquelles la moindre faute de frappe sera fatale.
Je sais pas si tu as du "bagage" en algèbre linéaire, mais je vais quand même te mettre aussi un minimum de théorie au moins au cas où quelqu'un veuille vérifier que je me suis pas gouré...
Pour mener les calculs, en fait seule les parties en bleu sont utile.

Les 9 valeurs cherchées , on peut les voir comme une matrice 3x3 .
Ensuite, si les 4 points "de contrôle" ont pour coordonnées avec et que les 4 points auxquels ils correspondent (obtenus lors de la phase de calibrage) ont pour coordonnées alors ce qu'on veut en fait, c'est que pour tout (avec )
Si on considère les matrices (connues) et ça signifie qu'il faut en particulier que où est une matrice diagonale (avec 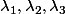) sur la diagonale.
Donc et la 4em équation dans laquelle on peut prendre (vu qu'il y a une infinité de solution) nous donne alors .
Donc, si et on doit prendre puis

Ensuite, une fois la matrice calculée, partant d'un point théorique , pour obtenir le point compensé , tu calcule et tu as tout simplement
Et si besoin est (par exemple pour savoir où est située en ce moment la tête d'écriture de ta table traçante en terme de coordonnées non compensée) pour avoir la fonction dans l'autre sens (x',y') -> (x,y) il te suffit de faire la même chose mais avec la matrice à la place de A.

[flamme34kloe]

Bonjour,
désolé de revenir temps de temps avant mais on m'a basculé de projet sans prévenir en cours de route.

Je connais vaguement les matrices pour en avoir utilisé mais jamais calculé.
je comprend qu'il faut calculer les valeur de a à j mais tu m'as perdu sur le comment.