Multiplicité algébrique et géométrique d'une valeur propre p

[Kinoa]

Bonjour tout le monde,

J'ai une question sur cet exercice, on me dit que la valeur propre de la matrice suivante est 1 :



Puis on demande de donner la multiplicité algébrique et géométrique de cette valeur propre.

Je remarque que la matrice est symétrique, mais mis à part cela, je ne vois pas comment trouver ces multiplicité sans écrire le polynôme caractéristique.. Ce qui à mon avis n'est clairement pas le but de cet exercice..

Une propriété m'échappe sûrement.

Merci d'avance pour votre aide :lol3:.

[Gathart]

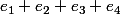
Valeur propre evidente 1 avec vecteur propre evident car la somme des colonnes vaut toujours 1.

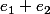
Ensuite tu as aussi vecteur propre de valeur propre 1 (somme des deux premiers colonnes seulement).

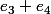
De même , or celui si se retouve par différence avec les deux du haut

Enfin

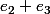
Donc 1 est valeur propre de vecteur propre les précédents donc de multiplicité 3.

voilà c'est bon ou plus d'explication ?

[Gathart]

Bon je m'exprime différement,

Il faut avoir l'habitude de voir les vecteurs propres dans ces cas évidents...







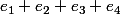
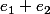
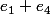
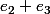
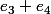
Cependant, mon espace propre a une base avec moins de vecteur.
Il faut regarder vite fais pour comprendre que c'est 3

[Gathart]

Ahh oui et maintenant on peut remarquer que 5 est valeur propre (par la trace) de vecteur propre (1,-1,1,-1)

[Gathart]

Ahh oui et maintenant on peut remarquer que 5 est valeur propre (par la trace) de vecteur propre (1,-1,1,-1)

On peut vérifier le résultat facilement...

[Kinoa]

Thanks !

(J'ai saisi :lol3:).