Statistiques

[Raph4767]

Y = AX + B

Avec A matrice 2x3
1 -3 0
4 2 1

B vecteur colonne de taille 2
0
1

[Ben314]

Salut,
J'y connais pas grand chose (pour ne pas dire rien...) au loi normales multidimensionnelles,mais je suis allé regarder la page de Wiki sur les loi normales multidimensionnelles pour y trouver la définition du bidule :
La loi c'est (par définition) celle de densité
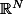où (et ) sont des éléments de vu comme des vecteurs colonne et où une matrice symétrique définie positive .

Vu qu'ici on est dans le cas où et, vue la définition de Wiki, ce qu'il faut que tu fasse, c'est de trouver et symétrique telles que, pour tout on ait soit encore en séparant termes quadratique/linéaires/constant.

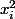- La partie quadratique donne et les coeff. en donnent et ceux en 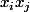donnent donc 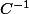est connue.

- La partie linéaire donne c'est à dire le système .
Comme on en a besoin ensuite, on peut commencer par calculer l'inverse de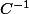 qui est (calculs) puis

- La partie constante donne et vu qu'on connait tout, c'est une simple vérification pour savoir si l'énoncé est cohérent (et/ou si on s'est gouré dans les calculs...)

Et il reste aussi à vérifier (toujours pour voir si l'énoncé est cohérent) que

Bref, jusque là, c'est de l'algèbre (bi)linéaire plutôt élémentaire.

Faire attention au fait que, vu que la partie constante correspond à un produit par , elle peut, si on veut, être mélangée ou regroupée avec le terme constant .

[Raph4767]

Merci infiniment !

[Raph4767]

Pour les lois de X1 X2 X3

Pour X1 suit la loi normale N(0,C1) avec C1 = ( 6 -3 -2 )' ?

Que signifie en déduire les moments d'ordre 2 de X?

Merci

[Ben314]

Pour X1 suit la loi normale N(0,C1) avec C1 = ( 6 -3 -2 )' ?

Surement pas vu que ça veut absolument rien dire ton truc : X1 c'est une variable aléatoire réelle (et pas vectorielle) donc je vois franchement pas ce que viendrait foutre un quelconque vecteur là dedans.

Que signifie en déduire les moments d'ordre 2 de X ?

Quand on lit des maths. (ou du Français...), c'est effectivement pas con de commencer par chercher la définition des mots du texte que l'on ne comprend pas.
Et dans le cas présent, ben faut espérer que c'est dans ton cours vu que j'y connais (toujours) rien.
J'aurais tendance à supposer que c'est les et les , mais c'est pas sûr...

[Raph4767]

Oui mais je ne vois pas comment le déduire de la matrice C...

[Raph4767]

Je crois avoir trouvé X1 suit N(0,6), X2 suit N(1,3), X3 suit N(2,3)

[Ben314]

Oui, je pense que c'est ça : le vecteur te donne les moyennes E(Xi) des composantes de X et la matrice C te donne les covariances Cov(Xi,Xj) donc en particulier, la diagonale te donne les variances V(Xi) des composantes.

[Raph4767]

Et donc les valeurs sur la diagonale ce sont les moments d'ordre 2... qui correspondent aux variances de X1,X2,X3, c'est cela ?

Pour la question 3. Je ne vois pas encore le lien avec ce qui est fait avant, je vais chercher.

[Ben314]

Si je me suis pas trop gouré, ton vecteur Y=(Y1,Y2), il suis une loi N2(n,D) où n=A.m+B et D=A.C.A^T

[Raph4767]

D=A.C.A^T

Pourquoi ?

[Ben314]

Le vecteur m et la matrice C trouvés précédemment correspondent en fait à : m=E(X) et C=E((X-m).(X-m)^T)
Comme Y=A.X+B on a
(1) n = E(Y) = E(A.X+B) = A.E(X)+B = A.m+B par linéarité de l'espérance.
(2) D = E((Y-n).(Y-n)^T) = E(A.(X-m).(A.(X-m))^T) = E(A.(X-m).(X-m)^T.A^T) = A.E((X-m).(X-m)^T).A^T=A.C.A^T toujours par linéarité de l'espérance.

Après, dans cette "preuve", ce qu'il manque c'est la justification que Y est lui même un vecteur gaussien (partant du fait que X en était déjà un). Y'a qu'à dire que "c'est connu"...