RESOLU : Vecteurs et triangle

[toushusss]

Bonjour, pourriez vous m'aider sur cet énoncé car je sèche complètement
J'ai un triangle ABC quelconque
et AI = 3/4 AB
BJ = 1/3 BC
CK = 2KA
(Le tout en vecteur)
Je dois démontrer que (AJ), (BK) et (CI) sont concourantes.
J'ai essayé de partir des relations AB + BC = AC
ou d'avoir un point d'intersection M entre (AJ) et (BK) et de montrer que M appartient aussi à (CI) mais je tourne en rond
Merci pour votre aide

[Pseuda]

Bonjour,

Une piste : se placer dans le repère (A, B, C), déterminer les coordonnées du point d'intersection des droites (AJ) et (BK) à l'aide de l'équation des droites, puis montrer que ce point appartient â la droite (CI).

[chombier]

As-tu fait une figure ? Si non fais en une.
Et montre là nous !
Merci d'avance

[toushusss]

Oui j'ai fait une figure, et sur celle ci on bien les 3 droites qui se coupent en un point
Le problème est de le démontrer,

[chombier]

Fais nous voir ta figure s'il te plait.

[toushusss]

Voilà

Triangle.png (207.25 Kio) Vu 929 fois

[chombier]

Dans ton énoncé tu disais

Cela ne corresponds pas avec ta figure.

Enoncé bidon. Je passe la main.

[toushusss]

Autant pour moi : 3CK = 2 KA

[chombier]

Comme l'a proposé pseuda, je me placerait dans le repère et de tout faire en géométrie analytique
- Chercher les coordonnées des points A, B, C, I, J, K dans ce repère
- Chercher les coordonnées du point M, intersection de (BK) et (IC) dans ce repère
- Puis démontrer que le point M appartient à la droite (AJ), par exemple en démontrant que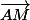 et 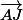sont colinéaires

[toushusss]

Merci pour les pistes c'est sympa.
Je cherche plutôt à le faire avec les relations entre vecteurs type relation de Chasles

[Pseuda]

Une autre solution (avec les vecteurs) : tu peux poser , et calculer 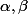en utilisant les données du problème.

Le souci c'est qu'il faut d'abord introduire le point M (sauf à deviner ses coordonnées dans le repère proposé) et montrer que ce point appartient aux 3 droites.

Sauf si tu as vu les barycentres : dans ce cas ce problème se résout très facilement avec l'associativité du barycentre.

[chombier]

Tu vas trimer ! Et Chasles ne va pas beaucoup t'aider.

Si M est l'intersection entre (AJ) et (BK), cela veux dire qu'il existe un unique couple de réels (a, b) tels que et .

Tu dois trouver les valeurs de a et b en résolvant un système (on y reviens).

Ensuite tu dois prouver qu'il existe un réel c tel que

Tu vas en baver et ça ne sera pas très beau. Je ne pense pas qu'il existe une méthode élégante n'utilisant que les vecteurs pour faire cet exercice.

[chombier]

Une autre solution (avec les vecteurs) : tu peux poser , et calculer en utilisant les données du problème.

Ca reviens au même, et sont les coordonnées de M
Après ce que je propose n'est pas non plus fondamentalement différent...
Comment prouver que 3 droites sont concourrantes... Il n'y a pas 50 méthodes...

[chombier]

Sauf si tu as vu les barycentres : dans ce cas ce problème se résout très facilement avec l'associativité du barycentre.

Ah oui, ça c'est joli. Mais pas si simple.

I est le barycentre de (A,3) ; (B, 1)
J est le barycentre de (B,2) ; (C,1)
K est le barycentre de (A,2) ; (C,3).

B est le barycentre de (A, 1) ; (I, -4) ainsi que le barycentre de (C,2) ; (J, -1)

Pas si simple... Comment introduire le point M ?

[siger]

bonsoir

la solution qui me semble la plus simple est celle qui a ete indiquee par Chombier: travailler dans le repere (A,AB,AC) dans lequel les coordonnees sont
A(0,0),B(0,1) , C(1,0), I(0,3/4),J(2/3,1/3) et K ( 1/3,0)
.......

pour utiliser les vecteurs et les barycentres comme indique par Pseuda, consulter "wikipedia": barycentre, reduction de fonctions vectorielles, exemple pratique"
M est le barycentre de (A,2) (B,6) et (C,3)
......

[chombier]

bonsoir
pour utiliser les vecteurs et les barycentres comme indique par Pseuda, consulter "wikipedia": barycentre, reduction de fonctions vectorielles, exemple pratique"

Ah oui, joli

I est le barycentre de { (A,1) ; (B, 3) } et donc de { (A, 2) ; (B, 6) }
J est le barycentre de { (B,2) ; (C,1) } et donc de { (B, 6) ; (C, 3) }
K est le barycentre de { (A,2) ; (C,3). } et donc de { (A, 2) ; (C, 3) }

M est le barycentre de { (A, 2) ; (B, 6) ; (C, 3) }. Ca me plait !!

[Pseuda]

Grâce à l'associativité du barycentre, on en déduit que M est à la fois le barycentre de :
(A ; 2) et (J ; 9)
(B; 6) et ( K; 5)
(C ;3) et ( I ; 8).
Donc les droites (AJ), (BK) et (CI) sont concourantes en M.

Et maintenant, pour une démonstration élégante sans connaître les barycentres, on peut traduire tout cela en termes de vecteurs.

[toushusss]

Bonjour,
Ok j'ai réussi avec les coordonnées des vecteurs.
Merci pour toutes les aides apportées.