Math dm

[ewen]

Bonjour, voici mon dm, besoin d'aide.

On doit découper une flèche dont la surface est de 0,5 m2, dans une planche de bois carrée de côté 1m comme représenté ci-dessous :
Combien doit mesurer le segment [DH] ?

[laetidom]

Bonjour,

Une image jointe ?

[ewen]

Bonjour,
Allez sur ce site: http://www.mathforu.com/sujet-22820.html
La figure est dessus.

[laetidom]

ABCD = 1 m²

AHH = (1-x)²/2

2.AHH = 2((1-x)²/2) = (1-x)²

Donc aire flèche = 1 - (1-x)² et de plus aire flèche = 0.5 m²

ça devrait pouvoir se résoudre . . . ====>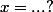 donc DH

[ewen]

Oui j'avait trouvé sa, mais après je sais pas résoudre 1-(1-x)²=0,5

[laetidom]

Oui j'avais trouvé ça, mais après je ne sais pas résoudre 1-(1-x)²=0,5

Oh ! ? . . .

Développe (1-x)², réduis . . .

(a - b)² = a² - 2ab + b²

[ewen]

Mais on ne trouve pas x car sa donne 1-2x+x²

[laetidom]

Mais on ne trouve pas x car ça donne 1-2x+x² ====> c'est une équation ! : . . . = . . .

1-(1-x)²=0,5

==================> 1 - (1 - 2x + x²) = 0,5

1 - 1 + 2x - x² = 0,5

====> ça te parle maintenant ?

Quelle(s) valeur(s) pour x . . . ?

[ewen]

Nn je comprend pas .
Avec 1-1+2x-x²=0,5 on fait comment pour trouver x ?
Dsl si je comprend rien

[laetidom]

Tu es d'accord avec . . . ?

En quelle classe es-tu ? En seconde ?

[ewen]

En seconde oui
Avec 1-1+2x-x²=0,5
On a 2x-x²-0,5=0
Plutôt je crois que ta inversé 2x et 0,5 ou 1/2

[laetidom]

En seconde oui
Avec 1-1+2x-x²=0,5
On a 2x-x²-0,5=0
Plutôt je crois que ta inversé 2x et 0,5 ou 1/2

Oui !

remarque : ta version et la mienne sont équivalentes !
La mienne a l'avantage de commencer par un + qui s'simplifie les choses . . .

As-tu vu la forme canonique ? d'une équation du second degré

[ewen]

Sa me dit rien

[laetidom]

Ca me dit rien

x² - 2x + 0,5 = 0

Si tu prends, pour l'instant, que x² - 2x :

et que tu connais (a - b)² = a² - 2ab + b²

x² - 2x ressemble à a² - 2ab

[ewen]

Oui et x on le trouve cmt

[laetidom]

Oui et x on le trouve cmt

x² - 2x + 0,5 = 0

Si tu prends, pour l'instant, que x² - 2x :

et que tu connais (a - b)² = a² - 2ab + b²

x² - 2x ressemble à a² - 2ab

donc x² - 2x tu peux l'écrire (x - 1)²

[ewen]

Oui

[Tiruxa47]

Bonjour,

Pourquoi développer si c'est ensuite pour remettre ss forme canonique ?

Il valait mieux garder le carré et l'isoler : (1 - x)² =1/2
c'est équivalent à 1 - x = racine carrée (1/2) , car 1-x est positif par hypothèse

[laetidom]

Bonjour,

Pourquoi développer si c'est ensuite pour remettre ss forme canonique ?

Il valait mieux garder le carré et l'isoler : (1 - x)² =1/2
c'est équivalent à 1 - x = racine carrée (1/2) , car 1-x est positif par hypothèse

Ah oui, effectivement !, c'est plus simple !

[ewen]

Oui je préfère comme sa