Merci d'avance et bonne année !
Nombres complexes
17 messages
- Page 1 sur 1
nombres complexes
Bonjour excusez moi mais j'ai vraiment besoin d'aide pour les exercices 2 et 3 je n'y arrive pas
Merci d'avance et bonne année !
Merci d'avance et bonne année !
- Fichiers joints
-
- Urgent svp
- 15841148_1263824783664110_42576759_n (1).jpg (36.56 Kio) Vu 450 fois
Re: nombres complexes
1) Méthode un peu longue poser z= x+iy et déterminer X et Y de Z = X =i Y puis résoudre Y = 0
2) un imaginaire pur est égal à l'opposé de son conjugué
2) un imaginaire pur est égal à l'opposé de son conjugué
Re: nombres complexes
i) écris que Z est imaginaire pur
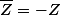
calcule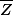 (la conjugaison est compatible avec toutes les opérations)
(la conjugaison est compatible avec toutes les opérations)
puis produit en croix
calcule
puis produit en croix
Re: nombres complexes
emma99 a écrit:pour l'exercice 2 ? merci beaucoup
pour l'exercice 3 poser z=x+iy
séparer les parties réelles et imaginaire.
On trouve l'équation d'une droite réelle
quel résultat obtiens tu pour l'exercice 2
Modifié en dernier par mathelot le 03 Jan 2017, 10:49, modifié 1 fois.
Re: nombres complexes
je trouve des resultats incoherents .... je n'ai peut etre pas la bonne technique
Re: nombres complexes
Pour l'exercice 3, tu peux poser 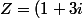 \bar{z}) , tu obtiens
, tu obtiens  , soit
, soit =-\frac52) puis tu remplaces Z par son expression avec z=x+iy
puis tu remplaces Z par son expression avec z=x+iy
Re: nombres complexes
pour l'exercice 2
Propriété: u est imaginaire pur ssi


par produit en croix et après réduction:
-4(z+\bar{z})=0)
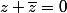 ou
ou -4=0)
z=x+iy
z imaginaire pur ou -2y-4=0
z imaginaire pur ou y=Im(z)=-2
Propriété: u est imaginaire pur ssi
par produit en croix et après réduction:
z=x+iy
z imaginaire pur ou -2y-4=0
z imaginaire pur ou y=Im(z)=-2
Re: nombres complexes
ah oui je comprend !
une dernière question, pour l'exercice 3, j'ai commencer avec le meme raisonnement mais cela ne fonctionne pas vraiment.....
une dernière question, pour l'exercice 3, j'ai commencer avec le meme raisonnement mais cela ne fonctionne pas vraiment.....
Re: nombres complexes
j'ai suivi les conseil de "sa majesté" mais cela ne fonctionne pas... je doit avoir un probleme
Re: nombres complexes
Bonsoir Emma99
Il faudrait que tu comprennes que l'on ne peut pas t'aider si tu ne prends pas la peine d'écrire ici tes calculs (au lieu de dire "mes calculs sont incohérents" ou " je n'y arrive pas").
Tu peux également remarquer que tes interlocuteurs, eux, ont pris la peine de détailler leur méthode ou leurs calculs ...
Il faudrait que tu comprennes que l'on ne peut pas t'aider si tu ne prends pas la peine d'écrire ici tes calculs (au lieu de dire "mes calculs sont incohérents" ou " je n'y arrive pas").
Tu peux également remarquer que tes interlocuteurs, eux, ont pris la peine de détailler leur méthode ou leurs calculs ...
Re: nombres complexes
oui desolé
pour l'exercice 3 j'ai poser Z=(1+3i)zbarre
Ensuite j'ai trouvé Z-Zbarre+5i et j'ai dit que c'etait egal a 0
Donc la partie imaginaire de Z est -5/2
Ce que je n'arrive pas c'est a remplacer Z par son expression z=x+iy
pour l'exercice 3 j'ai poser Z=(1+3i)zbarre
Ensuite j'ai trouvé Z-Zbarre+5i et j'ai dit que c'etait egal a 0
Donc la partie imaginaire de Z est -5/2
Ce que je n'arrive pas c'est a remplacer Z par son expression z=x+iy
Re: nombres complexes
oh mon dieu oui! je suis bete ! c'est la meilleure methode ? en tout cas c'est celle que je comprend le mieux. Quel chapitre difficile ...
merci beaucoup en tout cas
merci beaucoup en tout cas
Re: nombres complexes
emma99 a écrit:. Quel chapitre difficile ...
si tu veux un cours sur les complexes, http://www.olivier-bertrand.be/#/cours-en-ligne/3938020
bouton "Nbr complexes 1" et "Nbr complexes 2"
Re: nombres complexes
oh merci beaucoup ! encore de la gentillesse dans ce monde de fou. Merci pour tout
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
